2017年浙江省湖州市初二年级数学竞赛试卷本
试卷更新日期：2017-05-19 类型：竞赛测试
一、选择题
-
1. 一件商品进价为a元，商店将价格提高30%作零售价销售，在销售旺季过后，商店又以8折的价格开展促销活动.此时这件商品的售价为 （ ）A、a元 B、0.8a元 C、1.04a元 D、0.92a元2. 某学校为迎接市中学生足球赛，组织了学校班际足球比赛，下表是八年级A， B， C，D四个班举行足球単循环赛的成绩：
A班
B班
C班
D班
A班
×
0：1②
3：2
0：0
B班
1：0①
×
1：1
3：0
C班
2：3
1：1
×
4：1
D班
0：0
0：3
1：4
×
表中成绩栏中的比为所有球队比赛的进球之比.如①表示B班与A班的比赛中， B班以1：0获胜；②表示与①同一场比赛， A班输给了 B班.按规定，胜一场得3分，平一场得1分，负一场得0分，按得分由多到少排名次，则此次比赛的冠军队是 （ ）
A、A班 B、B班 C、C班 D、D班3. 小敏和小聪进行百米赛跑，小敏每秒跑6.3米，小聪每秒跑7.1米，小聪让小敏先跑5米，则比赛结果是（ ）
A、小敏和小聪同时到达终点 B、小敏比小聪早近1秒到达终点 C、小敏比小聪晚近1秒到达终点 D、小敏比小聪晚近0.9秒到达终点4.如图所示，在长方形ABCD的对称轴l上找点P，使得△PAB、△PBC、△PDC、△PAD均为等腰三角形，则满足条件的点P有.（ ）
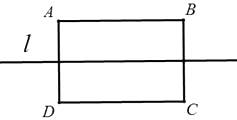A、5个 B、4个 C、3个 D、1个5.如图，四边形ABCD中，∠DAB=60°，∠B=∠D=90°， BC=1， CD=2，则对角线AC的长为（ ）
A、 B、 C、 D、6. 某校进行校园歌手大奖赛预赛，评委给每位选手打分时，最高分不超过10分，所有评委的评分中去掉一个最高分，去掉一个最低分后的平均分即为选手的最后得分.小敏的最后得分为9.68分，若只去掉一个最低分，小敏的得分为9.72分，若只去掉一个最高分，小敏的得分为9.66分，那么可以算出这次比赛的评委有（ ）A、9名 B、10名 C、11名 D、12名7.小敏尝试着将矩形纸片ABCD(如图①，AD>CD)沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE(如图②)； 再沿过D点的直线折叠， 使得 C点落在DA边上的点N处， E点落在AE边上的点M处，折痕为 DG(如图).如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD的长与宽的比值为（ ）
A、2 B、3 C、 D、8. 将1，2，3，4，5这五个数字排成一排，最后一个数是奇数，且使得其中任意连续三个数之和都能被这三个数中的第一个数整除，那么满足要求的排法有（ ）
A、2种 B、3种 C、4种 D、5种二、填空题
-
9.
如图，边长为1的正方形ABCD绕点A逆时针旋转30°到
正方形AB′C′D′，则围成图中阴影部分的周长和面积分别为
10. 在四边形ABCD(凸四边形)中， AB=AD=BC，∠BAD=90°，连结对角线 AC，当△ACD为等腰三角形时，则∠BCD的度数为11. 甲乙两地相距250km， 某天小颖从上午7： 50由甲地开车前往乙地办事.在上午9： 00， 10： 00， 11： 00这三个时刻， 车上的导航仪都进行了相同的提示： 如果按出发到现在的平均速度继续行驶，那么还有1个小时到达乙地. 如果导航仪的提示语都是正确的，那么在上午11：00时，小颖距乙地还有km.
12. 有一个正在向上匀速移动的自动扶梯， 旅客A从其顶端往下匀速行至其底端，共走了60级，B从其底端往上匀速行至其顶端，共走了30级(自动扶梯向上在行驶，两人也在梯上行走，且每次只跨l级)，且A的速度(即单位时间所走的级数)是B的速度的3倍， 那么该自动扶梯露在外面的级数是13. 设一次函数y=kx+2k-3(k≠0)，对于任意两个k的值k1 ， k2 ， 分别对应两个一次函数值y1 ， y2 ， 若k1k2<0，当x=m时，取相应y1 ， y2 ， 中的较小值p，则p的最大值是.14. 某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是角.三、解答题
-
15.
如图，在六边形的顶点处分别标上数1， 2， 3， 4，5， 6，能否使任意三个相邻顶点处的三个数之和
(1)、大于9?(2)、大于10?如能，请在图中标出来；若不能，请说明理由.
16. 某市对电话费作了调整,原市话费为每3分钟0.2元(不足3分钟按3分钟计算).调整后,前3分钟为0.2元,以后每分钟收0.1元(不足1分钟按1分钟计算).设通话时间x分钟时,调整前的话费为y1元,调整后的话费为y2元.(1)、当x=4, 4.3,5.8时,计算对应的话费值y1,y2各为多少,并指出x在什么范围取值时, y1≤y2?(2)、当x=m(m>5, m为常数)时,设计一种通话方案,使所需话费最小.17.如图，已知在△ABC中，AB=AC=10cm，BC=8cm，D为AB中点，设点P在线段BC上以3cm/秒的速度由B点向C点运动，点Q在线段CA上由C点向A点运动.
(1)、若Q点运动的速度与P点相同，且点P，Q同时出发，经过1秒钟后△BPD与△CQP是否全等，并说明理由；(2)、若点P，Q同时出发，但运动的速度不相同，当Q点的运动速度为多少时，能在运动过程中有△BPD与△CQP全等？(3)、若点Q以（2）中的速度从点C出发，点P以原来的速度从点B同时出发，都是逆时针沿△ABC的三边上运动，经过多少时间点P与点Q第一次在△ABC的哪条边上相遇？18.如图，直线y=kx-3与x轴、y轴分别交于点B，C， = .
(1)、求点B坐标和k值；(2)、若点A（x，y）是直线y=kx-3上在第一象限内的一个动点，当点A在运动过程中，试写出△AOB的面积S与x的函数关系式（不要求写自变量范围）；并进一步求出点A的坐标为多少时，△AOB的面积为 ？(3)、在上述条件下，x轴上是否存在点P，使△AOP为等腰三角形？若存在，请写出满足条件的所有P点坐标；若不存在，请说明理由.