广东省广州市海珠区2018-2019学年九年级下学期一模数学试卷

试卷更新日期：2019-05-14 类型：中考模拟

进入出卷网下载

一、选择题（满分30分）

1. -3的相反数为（）

A、-3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把不等式组 ${\begin{cases} x + 1 > 0 \\ 6 - 3 x \geq 0 \end{cases}$ 的解集表示在数轴上正确的是（）

A、 B、 C、 D、

查看试题解析
4. 在△ABC中，点D、E分别是边AB、AC的中点，DE=6，则BC=（）

A、3 B、6 C、9 D、12

查看试题解析
5. 在一次立定跳远的测试中，小娟等6位同学立定跳远的成绩分别为： 1.8、2、2.2、1.7、2、1.9，那么关于这组数据的说法正确的是（）

A、平均数是2 B、中位数是2 C、众数是2 D、方差是2

查看试题解析
6. 若一个正多边形的一个外角是30°，则这个正多边形的边数是（）

A、12 B、11 C、10 D、9

查看试题解析
7. 如图，AB∥DE，∠E=62°，则∠B+∠C等于（）

A、138° B、118° C、38° D、62°

查看试题解析
8. 对于二次函数 $y = - 2 x^{2} - 4 x + 1$ ，下列说法正确的是

A、当 $x < 0$ ，y 随x的增大而增大 B、当 x=-1 时，y有最大值3 C、图象的顶点坐标为 $(1 ， 3)$ D、图象与 x 轴有一个交点

查看试题解析
9. 已知圆锥的母线长是4cm，侧面积是12πcm² ，则这个圆锥底面圆的半径是（）

A、3cm B、 4cm C、5cm D、6cm

查看试题解析
10. 将抛物线 $y = x^{2} - 4 x + 1$ 向左平移至顶点落在y轴上，如图所示，则两条抛物线、直线y=-3和x轴围成的图形的面积S（图中阴影部分）是（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题（满分18分）

11. 分解因式： $2 a^{2} - 4 a b =$ ．

查看试题解析
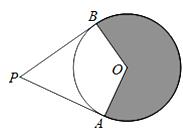
12. 计算： $\sqrt{9} + {(- 1)}^{2019} - 2 \sin 30^{\circ} =$ ．

查看试题解析
13. 已知命题：“如果两个角是直角，那么它们相等”，该命题的逆命题是命题（填“真”或“假”）．

查看试题解析
14. 已知一次函数图象经过第一、二、四象限，请写出一个符合条件的一次函数解析式．

查看试题解析
15. 如图，PA、PB是⊙O的两条切线，A、B是切点，PA= $\sqrt{3}$ OA，阴影部分的面积为6π，则⊙O的半径长为．

查看试题解析
16. 如图把矩形ABCD翻折，使得点A与BC边上的点G重合，折痕为DE，连结AG交DE于点F，若EF=1，DG= $\sqrt{6}$ ，则BE= ．

查看试题解析

三、解答题（满分102分）

17. 解分式方程： $\frac{1}{x - 4} - 2 = \frac{x}{4 - x}$ ．

查看试题解析
18. 如图，在▱ABCD中， BE、DF分别是∠ABC和∠CDA的平分线．求证：四边形BEDF是平行四边形．

查看试题解析
19. 先化简，再求值： ${(a + b)}^{2} + (a - b) (a + b) - 3 a^{2}$ ，其中 $a = - 2 \sqrt{2} ， b = \sqrt{2}$ ．

查看试题解析
20. 某校响应国家号召，鼓励学生积极参与体育锻炼．为了解学生一星期参与体育锻炼的时间情况，从全校2000名学生中，随机抽取50名学生进行调查，按参与体育锻炼的时间t（单位：小时），将学生分成五类：A类 $(0 \leq t \leq 2)$ ，B类 $(2 < t \leq 4)$ ，C类 $(4 < t \leq 6)$ ，D类 $(6 < t \leq 8)$ ，E类 $(t > 8)$ ．绘制成尚不完整的条形统计图如图．根据以上信息，解答下列问题：

(1)、样本中E 类学生有 ▲ 人，补全条形统计图；

(2)、估计全校的D类学生有人；

(3)、从该样本参与体育锻炼时间在 $0 \leq t \leq 4$ 的学生中任选2人，求这2人参与体育锻炼时间都在 $2 < t \leq 4$ 中的概率．

查看试题解析
21. 如图，楼房BD的前方竖立着旗杆AC．小亮在B处观察旗杆顶端C的仰角为45°，在D处观察旗杆顶端C的俯角为30°，楼高BD为20米．

(1)、求∠BCD的度数；

(2)、求旗杆AC的高度．

查看试题解析
22. 如图，已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O，∠B的平分线BE交AC于D，交⊙O于E，过E作EF∥AC交BA的延长线于F．

(1)、求证：EF是⊙O切线；

(2)、若AB=15，EF=10，求AE的长．

查看试题解析
23. 如图，双曲线 $y_{1} = \frac{k_{1}}{x}$ 与直线 $y_{2} = k_{2} x + b$ 相交于A $(1 ， m + 2)$ ，B $(4 ， m - 1)$ ，点P是x轴上一动点．

(1)、当 $y_{1} > y_{2}$ 时，直接写出 ${\begin{cases} k_{2} + b = 4 \\ 4 k_{2} + b = 1 \end{cases}$ 的取值范围；

(2)、求双曲线 $y_{1} = \frac{k_{1}}{x}$ 与直线 $y_{2} = k_{2} x + b$ 的解析式；

(3)、当△PAB是等腰三角形时，求点P的坐标．

查看试题解析
24. 如图，二次函数 $y = a x^{2} + c$ 的图象经过点 $A (- 1 ， \frac{5}{4})$ 和点 $C (- 4 ， 5)$ ，点 $B （ 0 ， 5 ）$

(1)、求二次函数 $y = a x^{2} + c$ 的解析式；

(2)、在图①中仅用尺规作图（保留作图痕迹，不要求写作法）在 $y$ 轴上确定点 $P$ ，使∠ $A P O$ =∠ $B P C$ ，直接写出点 $P$ 的坐标；

(3)、在（2）的条件下，如图②，过点P的直线 $y = k x + b$ 交二次函数 $y = a x^{2} + c$ 的图象于D $(x_{1} ， y_{1})$ ，E $(x_{2} ， y_{2})$ ，且 $x_{1} < 0 < x_{2}$ ，过点D、E作 ${\begin{cases} k_{2} + b = 4 \\ 4 k_{2} + b = 1 \end{cases}$ 轴的垂线段，垂足分别是F、G，连接PF、PG，
①求证：无论 $k$ 为何值，总有∠FPO=∠PGO；

②当PF+PG取最小值时，求点O到直线 $y = k x + b$ 的距离．

查看试题解析
25. 已知点A、B在⊙O上，∠AOB=90°，OA= $\sqrt{2}$ ，

(1)、点P是优弧 $\overset{⌢}{A B}$ 上的一个动点，求∠APB的度数；

(2)、如图①，当 $\tan ∠ O A P = \sqrt{2} - 1$ 时，求证： $∠ A P O = ∠ B P O$ ；

(3)、如图②，当点P运动到优弧 $\overset{⌢}{A B}$ 的中点时，点Q在 $\overset{⌢}{P B}$ 上移动（点Q不与点P、B重合），若△QPA的面积为 $S {}_{1}$ ，△QPB的面积为 $S {}_{2}$ ，求 $S {}_{1}+ S_{2}$ 的取值范围．

查看试题解析

广东省广州市海珠区2018-2019学年九年级下学期一模数学试卷

一、选择题（满分30分）

二、填空题（满分18分）

三、解答题 （满分102分）

三、解答题（满分102分）