广东省广州市南沙区2018-2019学年九年级下学期一模数学试卷
试卷更新日期:2019-05-14 类型:中考模拟
一、选择题(共30分)
-
1. 8的立方根是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是( )
 A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图,直线 ,以直线 上的点A为圆心、适当长为半径画弧,分别交直线 、 于点B、C,连接AC、BC.若∠ABC=65°,则∠1=( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图4. 如图,直线 ,以直线 上的点A为圆心、适当长为半径画弧,分别交直线 、 于点B、C,连接AC、BC.若∠ABC=65°,则∠1=( ) A、115° B、80° C、65° D、50°5. 南沙区某中学在备考2019广州中考体育的过程中抽取该校九年级20名男生进行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:
A、115° B、80° C、65° D、50°5. 南沙区某中学在备考2019广州中考体育的过程中抽取该校九年级20名男生进行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:成绩(单位:米)
2.10
2.20
2.25
2.30
2.35
2.40
2.45
2.50
人数
2
3
2
4
5
2
1
1
则下列叙述正确的是( )
A、这些男生成绩的众数是5 B、这些男生成绩的中位数是2.30 C、这些男生的平均成绩是2.25 D、这些男生成绩的极差是0.356. 下列数中与 最接近的是( )A、2 B、3 C、 D、47. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )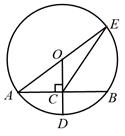 A、 B、8 C、 D、8. 港珠澳大桥是我国桥梁建筑史上的又一伟大奇迹,东接香港,西接珠海、澳门,全程 55千米.通车前需走水陆两路共约 170 千米,通车后,约减少时间3小时,平均速度是原来的 倍,如果设原来通车前的平均时速为 千米/小时,则可列方程为( )A、 B、 C、 D、9. 在同一直角坐标系中,一次函数 和二次函数 的大致图象是( )A、
A、 B、8 C、 D、8. 港珠澳大桥是我国桥梁建筑史上的又一伟大奇迹,东接香港,西接珠海、澳门,全程 55千米.通车前需走水陆两路共约 170 千米,通车后,约减少时间3小时,平均速度是原来的 倍,如果设原来通车前的平均时速为 千米/小时,则可列方程为( )A、 B、 C、 D、9. 在同一直角坐标系中,一次函数 和二次函数 的大致图象是( )A、 B、
B、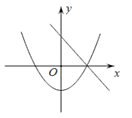 C、
C、 D、
D、 10. 如图,在直角坐标系中,有一等腰直角三角形OBA,∠OBA=90°,斜边OA在x轴正半轴上,且OA=2,将Rt△OBA绕原点O逆时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OB1A1(即A1O=2AO).同理,将Rt△OB1A1逆时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OB2A2……依此规律,得到等腰直角三角形OB2019A2019 , 则点B2019的坐标为( )
10. 如图,在直角坐标系中,有一等腰直角三角形OBA,∠OBA=90°,斜边OA在x轴正半轴上,且OA=2,将Rt△OBA绕原点O逆时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OB1A1(即A1O=2AO).同理,将Rt△OB1A1逆时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OB2A2……依此规律,得到等腰直角三角形OB2019A2019 , 则点B2019的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共18分)
-
11. 关于 的不等式组的解集在数轴上的表示如图所示,则此不等式组的解集为 .
 12. 抛物线 的顶点坐标是 .13. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的余弦值等于 .
12. 抛物线 的顶点坐标是 .13. 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的余弦值等于 . 14. 如图,在平行四边形ABCD中,BE⊥AC,AC=24,BE=5,AD=8,则两平行线AD与BC间的距离是 .
14. 如图,在平行四边形ABCD中,BE⊥AC,AC=24,BE=5,AD=8,则两平行线AD与BC间的距离是 . 15. 如果 ,则 的值为 .16. 如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,BG=6GF;⑤S四边形BCDG= .其中正确的结论有(填序号).
15. 如果 ,则 的值为 .16. 如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,BG=6GF;⑤S四边形BCDG= .其中正确的结论有(填序号).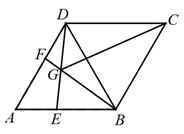
三、解答题(满分102分)
-
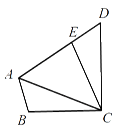
17. 解一元一次方程: .18. 如图,已知在四边形ABCD中,点E在AD上,∠B+∠AEC=180°,∠BAC=∠D,BC=CE.求证:AC=DC.
 19. 已知(1)、化简 ;(2)、若 为△ABC的面积,其中∠C=90°,∠A=30°,BC=2,求T的值.20. 随着中国传统节日“端午节”的临近,永旺超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买1盒甲品牌粽子和2盒乙品牌粽子需230元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.(1)、打折前甲、乙两种品牌粽子每盒分别为多少元?(2)、阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?21. 随着信息技术的快速发展,人们购物的付款方式更加多样、便捷.某校数学兴趣小组为了解人们最喜欢的付款方式设计了一份调查问卷,要求被调查者选且只选其中一种你最喜欢的付款方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请根据统计图回答下列问题:
19. 已知(1)、化简 ;(2)、若 为△ABC的面积,其中∠C=90°,∠A=30°,BC=2,求T的值.20. 随着中国传统节日“端午节”的临近,永旺超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买1盒甲品牌粽子和2盒乙品牌粽子需230元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.(1)、打折前甲、乙两种品牌粽子每盒分别为多少元?(2)、阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?21. 随着信息技术的快速发展,人们购物的付款方式更加多样、便捷.某校数学兴趣小组为了解人们最喜欢的付款方式设计了一份调查问卷,要求被调查者选且只选其中一种你最喜欢的付款方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请根据统计图回答下列问题:
 (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”付款的扇形圆心角的度数为;(2)、补全条形统计图;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种付款方式中选一种方式进行付款,请用树状图或列表法求出两人恰好选择同一种付款方式的概率.22. 已知直线 与直线 关于原点O对称,若反比例函数 的图象与直线 交于A、B两点,点A横坐标为1,点B纵坐标为 .(1)、求 , 的值;(2)、结合图象,当 时,求自变量 的取值范围.23. 如图,AB为 的直径,点C在 上,且tan∠ABC=2;
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”付款的扇形圆心角的度数为;(2)、补全条形统计图;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种付款方式中选一种方式进行付款,请用树状图或列表法求出两人恰好选择同一种付款方式的概率.22. 已知直线 与直线 关于原点O对称,若反比例函数 的图象与直线 交于A、B两点,点A横坐标为1,点B纵坐标为 .(1)、求 , 的值;(2)、结合图象,当 时,求自变量 的取值范围.23. 如图,AB为 的直径,点C在 上,且tan∠ABC=2; (1)、利用尺规过点A作 的切线AD(点D在直线AB右侧),且AD=AB,连接OD交AC于点E(保留作图痕迹,不写作法);(2)、在(1)条件下,
(1)、利用尺规过点A作 的切线AD(点D在直线AB右侧),且AD=AB,连接OD交AC于点E(保留作图痕迹,不写作法);(2)、在(1)条件下,①求证:OD∥BC;
②连接BD交 于点F,求证: .
24. 抛物线L: 经过点 ,与它的对称轴直线 交于点B.
 (1)、求出抛物线L的解析式;(2)、如图1,过定点的直线 与抛物线L交于点M、N.若△BMN的面积等于3,求k的值;(3)、如图2,将抛物线L向下平移m(m>0)个单位长度得到抛物线L1 , 抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.点F为抛物线L1的对称轴与x轴的交点,P为线段 上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.25. 如图1,已知在平面直角坐标系中,点O为坐标原点,点A在 轴负半轴上,直线 与 轴、 轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°.
(1)、求出抛物线L的解析式;(2)、如图1,过定点的直线 与抛物线L交于点M、N.若△BMN的面积等于3,求k的值;(3)、如图2,将抛物线L向下平移m(m>0)个单位长度得到抛物线L1 , 抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.点F为抛物线L1的对称轴与x轴的交点,P为线段 上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.25. 如图1,已知在平面直角坐标系中,点O为坐标原点,点A在 轴负半轴上,直线 与 轴、 轴分别交于B、C两点,四边形ABCD为平行四边形,且AC=BC,点P为△ACD内一点,连接AP、BP且∠APB=90°. (1)、求证:∠PAC=∠PBC;(2)、如图2,点E在线段BP上,点F在线段AP上,且AF=BE,∠AEF=45°,求 的值;(3)、在(2)的条件下,当PE=BE时,求点P的坐标.
(1)、求证:∠PAC=∠PBC;(2)、如图2,点E在线段BP上,点F在线段AP上,且AF=BE,∠AEF=45°,求 的值;(3)、在(2)的条件下,当PE=BE时,求点P的坐标.