湖南省郴州市2018年中考数学试卷
试卷更新日期:2019-05-13 类型:中考真卷
一、单选题
-
1. 下列实数:3、0、 、- 、0.35,其中最小的实数是( )A、3 B、0 C、- D、0.352. 郴州市人民政府提出:在2018年继续办好一批民生实事,加快补齐影响群众生活品质的短板,推进扶贫惠民工程,实线12.5万人脱贫,请用科学记数法表示125000为( )。A、1.25×105 B、0.125×106 C、12.5×104 D、1.25×1063. 下列运算正确的是( )A、a3·a2=a6 B、a-2=- C、 D、(a+2)(a-2)=a2+44. 如图,直线a,b被直线c所截,下列条件中,不能判定a∥b( )
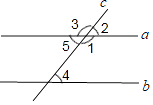 A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠35. 如图是由四个相同的小正方体搭成的立体图形,它的主视图是( )
A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠35. 如图是由四个相同的小正方体搭成的立体图形,它的主视图是( )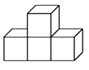 A、
A、 B、
B、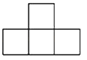 C、
C、 D、
D、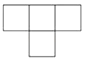 6. 甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )
6. 甲、乙两超市在1月至8月间的盈利情况统计图如图所示,下面结论不正确的是( )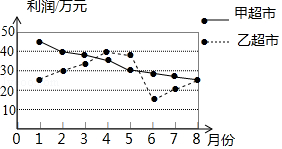 A、甲超市的利润逐月减少 B、乙超市的利润在1月至4月间逐月增加 C、8月份两家超市利润相同 D、乙超市在9月份的利润必超过甲超市7. 如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于 CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为( )
A、甲超市的利润逐月减少 B、乙超市的利润在1月至4月间逐月增加 C、8月份两家超市利润相同 D、乙超市在9月份的利润必超过甲超市7. 如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于 CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为( )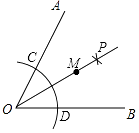 A、6 B、2 C、3 D、8. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
A、6 B、2 C、3 D、8. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )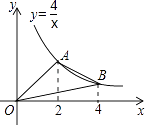 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 计算: =。10. 因式分解:a3-2a2b+ab2=。11. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。12. 在创建“平安校园”活动中,郴州市某中学组织学生干部在校门口值日,期中八位同学3月份值日的次数分别是:5,8,7,7,8,6,8,9,则这组数据的众数是。13. 已知关于x的一元二次方程x2+kx-6=0有一个根为-3,则方程的另一个根为。14. 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验,结果如下表所示,

则这个厂生产的瓷砖是合格品的概率估计值是。(精确到0.01)
15. 如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为cm.(结果用π表示) 16. 如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是 .
16. 如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是 .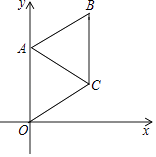
三、解答题
-
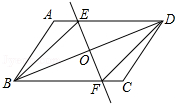
17. 计算:18. 解不等式组: ,并把解集在数轴上表示出来.19. 如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
 20. 6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
20. 6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:血型
A
B
AB
O
人数
10
5
 (1)、这次随机抽取的献血者人数为人,m=;
(1)、这次随机抽取的献血者人数为人,m=;
(2)、补全上表中的数据;
(3)、若这次活动中该市有3000人义务献血,请你根据抽样结果回答:从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?
21. 郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者。如果购买A种20件,B种1件,共需380圆;如果购买A种15件,B种10件,共需280元。(1)、A、B两种奖品每件各多少元?(2)、现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?22. 小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据: ≈1.414, ≈1.732)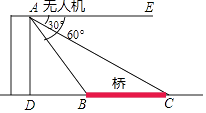 23. 已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
23. 已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°. (1)、求证:直线AD是⊙O的切线;(2)、若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
(1)、求证:直线AD是⊙O的切线;(2)、若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
24. 参照学习函数的过程与方法,探究函数y= 的图象与性质.因为y= ,即y=﹣ +1,所以我们对比函数y=﹣ 来探究.
列表:
x
…
﹣4
﹣3
﹣2
﹣1
﹣
1
2
3
4
…
y=﹣
…
1
2
4
﹣4
﹣1
1
﹣
﹣
…
y=
…
2
3
5
﹣3
﹣1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y= 相应的函数值为纵坐标,描出相应的点,如图所示:
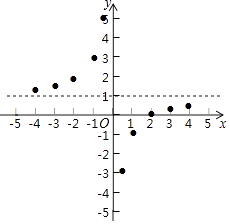 (1)、请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(1)、请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)、观察图象并分析表格,回答下列问题:①当x<0时,y随x的增大而;(填“增大”或“减小”)
②y= 的图象是由y=﹣ 的图象向平移个单位而得到;
③图象关于点中心对称.(填点的坐标)
(3)、设A(x1 , y1),B(x2 , y2)是函数y= 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
25. 如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.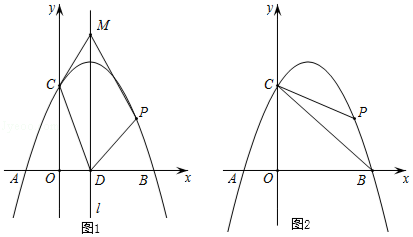 (1)、求抛物线的表达式;(2)、设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)、如图2,连接BC,PB,PC,设△PBC的面积为S.①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.
26. 在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.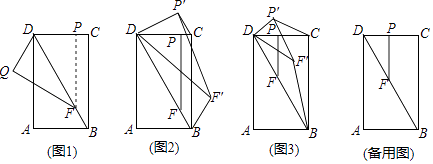 (1)、如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;(2)、如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
(1)、如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;(2)、如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.