2013年江苏省连云港市中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列各数中是正数的为（）

A、3 B、﹣ $\frac{1}{2}$ C、﹣ $\sqrt{2}$ D、0

查看试题解析
2. 计算a²•a⁴的结果是（）

A、a⁸ B、a⁶ C、2a⁶ D、2a⁸

查看试题解析
3. 将一包卷筒卫生纸按如图所示的方式摆放在水平桌面上，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 为了传承和弘扬港口文化，我市将投入6000万元建设一座港口博物馆，其中“6000万”用科学记数法表示为（）

A、0.6×10⁸ B、6×10⁸ C、6×10⁷ D、60×10⁶

查看试题解析
5. 在Rt△ABC中，∠C=90°，若sinA= $\frac{5}{13}$ ，则cosA的值为（）

A、 $\frac{5}{12}$ B、 $\frac{8}{13}$ C、 $\frac{2}{3}$ D、 $\frac{12}{13}$

查看试题解析
6. 如图，数轴上的点A、B分别对应实数a、b，下列结论中正确的是（）

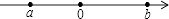A、a＞b B、|a|＞|b| C、﹣a＜b D、a+b＜0

查看试题解析
7. 在一个不透明的布袋中，红球、黑球、白球共有若干个，除颜色外，形状、大小、质地等完全相同，小新从布袋中随机摸出一球，记下颜色后放回布袋中，摇匀后再随机摸出一球，记下颜色，…如此大量摸球实验后，小新发现其中摸出红球的频率稳定于20%，摸出黑球的频率稳定于50%，对此实验，他总结出下列结论：①若进行大量摸球实验，摸出白球的频率稳定于30%，②若从布袋中任意摸出一个球，该球是黑球的概率最大；③若再摸球100次，必有20次摸出的是红球．其中说法正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析
8. 如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（）

A、1 B、 $\sqrt{2}$ C、4﹣2 $\sqrt{2}$ D、3 $\sqrt{2}$ ﹣4

查看试题解析

二、填空题

9. 计算：3²=

查看试题解析
10. 使式子 $\sqrt{x + 1}$ 有意义的x取值范围是．

查看试题解析
11. 分解因式：4﹣x²= ．

查看试题解析
12. 若正比例函数y=kx（k为常数，且k≠0）的函数值y随着x的增大而减小，则k的值可以是．（写出一个即可）

查看试题解析
13. 据市房管局统计，今年某周我市8个县区的普通住宅成交量如下表：
区县
赣榆
东海
灌云
灌南
新浦
海州
连云港
开发区
成交量（套）
105
101
53
72
110
50
56
88
则该周普通住宅成交量的中位数为套．

查看试题解析
14. 如图，一束平行太阳光线照射到正五边形上，则∠1= ．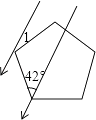

查看试题解析
15. 如图，△ABC内接于⊙O，∠ACB=35°，则∠OAB= ．

查看试题解析
16.
点O在直线AB上，点A₁、A₂、A₃ ， …在射线OA上，点B₁、B₂、B₃ ， …在射线OB上，图中的每一个实线段和虚线段的长均为一个单位长度，一个动点M从O点出发，按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动，速度为每秒1个单位长度，按此规律，则动点M到达A₁₀₁点处所需时间为秒．

查看试题解析

三、解答题

17. 计算（ $\frac{1}{5}$ ）^﹣¹+（ $\sqrt{2}$ ﹣1）⁰+2×（﹣3）

查看试题解析
18. 解不等式组 ${\begin{cases} x - 5 < 1 \\ x + 2 \leq 4 x - 7 \end{cases}}$ ．

查看试题解析
19. 先化简，再求值：（ $\frac{1}{m}$ ﹣ $\frac{1}{n}$ ）÷ $\frac{m^{2} - 2 m n + n^{2}}{m n}$ ，其中m=﹣3，n=5．

查看试题解析
20. 某校为了解“理化生实验操作”考试的备考情况，随机抽取了一部分九年级学生进行测试，测试结果分为“优秀”、“良好”、“合格”、“不合格”四个等级，分别记为A、B、C、D．根据测试结果绘制了如下尚不完整的统计图．

(1)、本次测试共随机抽取了名学生．请根据数据信息补全条形统计图；

(2)、若该校九年级的600名学生全部参加本次测试，请估计测试成绩等级在合格以上（包括合格）的学生约有多少人？

查看试题解析
21. 甲、乙、丙三人之间相互传球，球从一个人手中随机传到另外一个人手中，共传球三次．

(1)、若开始时球在甲手中，求经过三次传球后，球传回到甲手中的概率是多少？

(2)、若乙想使球经过三次传递后，球落在自己手中的概率最大，乙会让球开始时在谁手中？请说明理由．

查看试题解析
22. 在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．

(1)、求证：四边形BFDE为平行四边形；

(2)、若四边形BFDE为菱形，且AB=2，求BC的长．

查看试题解析
23. 小林准备进行如下操作实验；把一根长为40cm的铁丝剪成两段，并把每一段各围成一个正方形．

(1)、要使这两个正方形的面积之和等于58cm² ，小林该怎么剪？

(2)、小峰对小林说：“这两个正方形的面积之和不可能等于48cm² ． ”他的说法对吗？请说明理由．

查看试题解析
24.
如图，已知一次函数y=2x+2的图象与y轴交于点B，与反比例函数y= $\frac{k_{1}}{x}$ 的图象的一个交点为A（1，m）．过点B作AB的垂线BD，与反比例函数y= $\frac{k_{2}}{x}$ （x＞0）的图象交于点D（n，﹣2）．

(1)、求k₁和k₂的值；

(2)、若直线AB、BD分别交x轴于点C、E，试问在y轴上是否存在一个点F，使得△BDF∽△ACE？若存在，求出点F的坐标；若不存在，请说明理由．

查看试题解析
25. 我市某海域内有一艘轮船发生故障，海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援，与故障渔船会合后立即将其拖回．如图折线段O﹣A﹣B表示救援船在整个航行过程中离港口的距离y（海里）随航行时间x（分钟）的变化规律．抛物线y=ax²+k表示故障渔船在漂移过程中离港口的距离y（海里）随漂移时间x（分钟）的变化规律．已知救援船返程速度是前往速度的 $\frac{2}{3}$ ．根据图象提供的信息，解答下列问题：

(1)、救援船行驶了海里与故障船会合；

(2)、求该救援船的前往速度；

(3)、若该故障渔船在发出求救信号后40分钟内得不到营救就会有危险，请问救援船的前往速度每小时至少是多少海里，才能保证故障渔船的安全．

查看试题解析
26. 如图，在平面直角坐标系中，O为坐标原点，点A、B的坐标分别为（8，0）、（0，6）．动点Q从点O、动点P从点A同时出发，分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动，运动时间为t（秒）（0＜t≤5）．以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连接CD、QC．

(1)、求当t为何值时，点Q与点D重合？

(2)、设△QCD的面积为S，试求S与t之间的函数关系式，并求S的最大值；

(3)、若⊙P与线段QC只有一个交点，请直接写出t的取值范围．

查看试题解析
27.
小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：
问题情境：如图1，四边形ABCD中，AD∥BC，点E为DC边的中点，连接AE并延长交BC的延长线于点F，求证：S_四边形_ABCD=S_△_ABF ．（S表示面积）
问题迁移：如图2：在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．小明将直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值，请问当直线MN在什么位置时，△MON的面积最小，并说明理由．
实际应用：如图3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB=66°，∠POB=30°，OP=4km，试求△MON的面积．（结果精确到0.1km²）（参考数据：sin66°≈0.91，tan66°≈2.25， $\sqrt{3}$ ≈1.73）
拓展延伸：如图4，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）（6，3）（ $\frac{9}{2}$ ， $\frac{9}{2}$ ）、（4、2），过点p的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．

查看试题解析

区县	赣榆	东海	灌云	灌南	新浦	海州	连云港	开发区
成交量（套）	105	101	53	72	110	50	56	88