2012年江苏省盐城市中考数学试卷
试卷更新日期：2017-05-18 类型：中考真卷
一、选择题
-
1. ﹣2的倒数是（ ）
A、2 B、﹣2 C、 D、﹣2. 4的平方根是（ ）A、2 B、16 C、±2 D、±163. 如图是一个由3个相同的正方体组成的立体图形，则它的主视图为（ ）
A、
B、
C、
D、
4. 下面四个实数中，是无理数的为（ ）A、0 B、 C、﹣2 D、5. 一只因损坏而倾斜的椅子，从背后看到的形状如图，其中两组对边的平行关系没有发生变化，若∠1=75°，则∠2的大小是（ ）
A、75° B、115° C、65° D、105°6. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是 =0.90， =1.22， =0.43， =1.68，在本次射击测试中，成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁7. 已知整数a1 ， a2 ， a3 ， a4 ， …满足下列条件：a1=0，a2=﹣|a1+1|，a3=﹣|a2+2|，a4=﹣|a3+3|，…，依此类推，则a2012的值为（ ）A、﹣1005 B、﹣1006 C、﹣1007 D、﹣2012二、填空题
-
8. 若二次根式 有意义，则x的取值范围是 ．9. 分解因式：a2﹣4b2=10. 中国共产党第十八次全国代表大会将于2012年10月15日至18日在北京召开．据统计，截至2011年底，全国的共产党员人数已超过80300000，这个数据用科学记数法可表示为 ．11. 若x=﹣1，则代数式x3﹣x2+4的值为12. 小勇第一次抛一枚质地均匀的硬币时正面向上，他第二次再抛这枚硬币时，正面向上的概率是 ．13. 若反比例函数的图象经过点P（﹣1，4），则它的函数关系式是 ．14. 如图，在四边形ABCD中，已知AB∥DC，AB=DC．在不添加任何辅助线的前提下，要想该四边形成为矩形，只需再加上的一个条件是 ． （填上你认为正确的一个答案即可）
15. 如图，在△ABC中，D、E分别是边AB、AC的中点，∠B=50°．先将△ADE沿DE折叠，点A落在三角形所在平面内的点为A1 ， 则∠BDA1的度数为 ．
16. 已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根，且圆心距O1O2=t+2，若这两个圆相切，则t= ．17. 一批志愿者组成了一个“爱心团队”，专门到全国各地巡回演出，以募集爱心基金．第一个月他们就募集到资金1万元．随着影响的扩大，第n（n≥2）个月他们募集到的资金都将会比上个月增加20%，则当该月所募集到的资金首次完成突破10万元时，相应的n的值为 ． （参考数据：1.25≈2.5，1.26≈3.0，1.27≈3.6）三、解答题
-
18.(1)、计算：|﹣ |﹣20120﹣sin30°；(2)、化简：（a﹣b）2+b（2a+b）．19. 解方程： ．20. 现有形状、大小、颜色完全一样的三张卡片，上面分别标有数字“1”、“2”、“3”，第一次从这三张卡片中随机抽取一张，记下数字后放回；第二次在从这三张卡片中随机抽取一张并记下数字．请用列表或画树状图的方法表示出上述试验所有可能的结果，并求第二次抽取的数字大于第一次抽取的数字的概率．21. 第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行，目前正在进行火炬传递活动．某校学生会为了确定近期宣传专刊的主题，想知道学生对伦敦奥运会火炬传递路线的了解程度，决定随机抽取部分学生进行一次问卷调查，并根据收集到的信息进行了统计，绘制了如图两幅上不完整的统计图．请你根据统计图中所提供的信息解答下列问题：
(1)、接受问卷调查的学生共有名；(2)、请补全折线统计图，并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小；(3)、若该校共有1200名学生，请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数．22. 如图所示，在梯形ABCD中，AD∥BC，∠BDC=90°，E为BC上一点，∠BDE=∠DBC．
(1)、求证：DE=EC；(2)、若AD= BC，试判断四边形ABED的形状，并说明理由．23.如图所示，当小华站立在镜子EF前A处时，他看自己的脚在镜中的像的俯角为45°．若小华向后退0.5米到B处，这时他看自己的脚在镜中的像的俯角为30°．求小华的眼睛到地面的距离．（结果精确到0.1米，参考数据： ≈1.73）
24. 如图①所示，已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1 ， 过点E作EE1⊥l于点E1 ．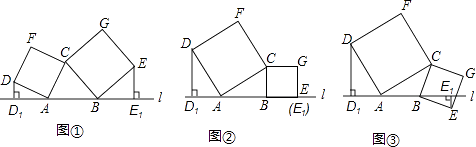
(1)、如图②，当点E恰好在直线l上时（此时E1与E重合），试说明DD1=AB；(2)、在图①中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；(3)、如图③，当点E在直线l的下方时，请直接写出三条线段DD1、EE1、AB之间的数量关系．（不需要证明）25. 如图所示，AC⊥AB，AB=2 ，AC=2，点D是以AB为直径的半圆O上一动点，DE⊥CD交直线AB于点E，设∠DAB=α（0°＜α＜90°）．
(1)、当α=18°时，求 的长；(2)、当α=30°时，求线段BE的长；(3)、若要使点E在线段BA的延长线上，则α的取值范围是（直接写出答案）26. 知识迁移当a＞0且x＞0时，因为 ，所以x﹣ + ≥0，从而x+ ≥ （当x= ）是取等号）．
记函数y=x+ （a＞0，x＞0）．由上述结论可知：当x= 时，该函数有最小值为2 ．
直接应用
已知函数y1=x（x＞0）与函数y2= （x＞0），则当x=1时，y1+y2取得最小值为2．
变形应用
已知函数y1=x+1（x＞﹣1）与函数y2=（x+1）2+4（x＞﹣1），求 的最小值，并指出取得该最小值时相应的x的值．
实际应用
已知某汽车的一次运输成本包含以下三个部分，一是固定费用，共360元；二是燃油费，每千米1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001．设该汽车一次运输的路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？
27.在平面直角坐标系xOy中，已知二次函数y= 的图象经过点A（2，0）和点B（1，﹣ ），直线l经过抛物线的顶点且与y轴垂直，垂足为Q．
(1)、求该二次函数的表达式；(2)、设抛物线上有一动点P从点B处出发沿抛物线向上运动，其纵坐标y1随时间t（t≥0）的变化规律为y1=﹣ +2t．现以线段OP为直径作⊙C．①当点P在起始位置点B处时，试判断直线l与⊙C的位置关系，并说明理由；在点P运动的过程中，直线l与⊙C是否始终保持这种位置关系？请说明你的理由．
②若在点P开始运动的同时，直线l也向上平行移动，且垂足Q的纵坐标y2随时间t的变化规律为y2=﹣1+3t，则当t在什么范围内变化时，直线l与⊙C相交？此时，若直线l被⊙C所截得的弦长为a，试求a2的最大值．