2016年广东省深圳市高考数学二模试卷（理科）

试卷更新日期：2017-05-18 类型：高考模拟

进入出卷网下载

一、选择题

1. 若复数z满足（1+i）z=1﹣i（i为虚数单位），则|z|=（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、2 D、1

查看试题解析
2. 设A，B是两个集合，则“x∈A”是“x∈（A∩B）”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 若coa（ $\frac{π}{2}$ ﹣α）= $\frac{1}{3}$ ，则cos（π﹣2α）=（）

A、﹣ $\frac{4 \sqrt{2}}{9}$ B、 $\frac{4 \sqrt{2}}{9}$ C、﹣ $\frac{7}{9}$ D、 $\frac{7}{9}$

查看试题解析
4. 若实数x，y满足约束条件 ${\begin{cases} x + y - 1 \geq 0 \\ x - 1 \leq 0 \\ 4 x - y + 1 \geq 0 \end{cases}$ 则目标函数z= $\frac{y + 1}{x + 3}$ 的最大值为（）

A、 $\frac{1}{4}$ B、 $\frac{2}{3}$ C、 $\frac{3}{2}$ D、2

查看试题解析
5. 在如图所示的流程图中，若输入a，b，c的值分别为2，4，5，则输出的x=（）

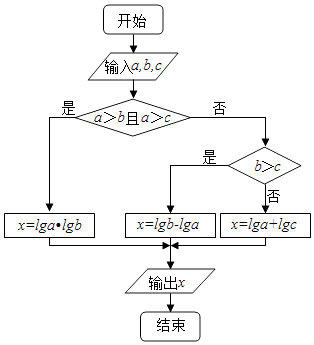A、1 B、2 C、lg2 D、10

查看试题解析
6. 已知函数f（x）的图象是由函数g（x）=cosx的图象经过如下变换得到：先将g（x）的图象向右平移 $\frac{π}{3}$ 个单位长度，再将其图象上所有点的横坐标变为原来的一半，纵坐标不变，则函数f（x）的图象的一条对称轴方程为（）

A、x= $\frac{π}{6}$ B、x= $\frac{5 π}{12}$ C、x= $\frac{π}{3}$ D、x= $\frac{7 π}{12}$

查看试题解析
7. 以直线y=± $\sqrt{3}$ x为渐近线的双曲线的离心率为（）

A、2 B、 $\frac{2 \sqrt{3}}{3}$ C、2或 $\frac{2 \sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
8. 2位男生和3位女生共5位同学站成一排，则3位女生中有且只有两位女生相邻的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
9. 如图，正方形ABCD中，M、N分别是BC、CD的中点，若 $\vec{A C}$ =λ $\vec{A M}$ +μ $\vec{B N}$ ，则λ+μ=（）

A、2 B、 $\frac{8}{3}$ C、 $\frac{6}{5}$ D、 $\frac{8}{5}$

查看试题解析
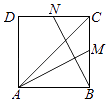10. 已知f（x）= ${\begin{cases} - \ln x - x ， x > 0 \\ - \ln (- x) + x ， x < 0 \end{cases}$ ，则关于m的不等式f（ $\frac{1}{m}$ ）＜ln $\frac{1}{2} - 2$ 的解集为（）

A、（0， $\frac{1}{2}$ ） B、（0，2） C、（﹣ $\frac{1}{2}$ ，0）∪（0， $\frac{1}{2}$ ） D、（﹣2，0）∪（0，2）

查看试题解析
11. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则它的体积为（）

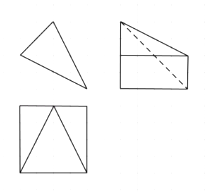A、48 B、16 C、32 D、16 $\sqrt{5}$

查看试题解析
12. 设定义在（0，+∞）上的函数f（x）满足xf′（x）﹣f（x）=xlnx，f（ $\frac{1}{e}$ ）= $\frac{1}{e}$ ，则f（x）（）

A、有极大值，无极小值 B、有极小值，无极大值 C、既有极大值，又有极小值 D、既无极大值，也无极小值

查看试题解析

二、填空题

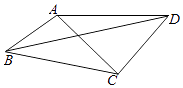
13. 高为π，体积为π²的圆柱体的侧面展开图的周长为．

查看试题解析
14. 过点P（3，1）的直线l与圆C：（x﹣2）²+（y﹣2）²=4相交于A，B两点，当弦AB的长取最小值时，直线l的倾斜角等于．

查看试题解析
15. 在（2+ $\sqrt{x}$ ﹣ $\frac{1}{x^{2016}}$ ）¹⁰的展开式中，x⁴项的系数为（结果用数值表示）．

查看试题解析
16. 如图，在凸四边形ABCD中，AB=1，BC= $\sqrt{3}$ ，AC⊥CD，AC=CD，当∠ABC变化时，对角线BD的最大值为．

查看试题解析

三、解答题

17. 设数列{a_n}的前n项和为S_n ， a_n是S_n和1的等差中项．

(1)、求数列{a_n}的通项公式；

(2)、求数列{na_n}的前n项和T_n ．

查看试题解析
18. 某市在对学生的综合素质评价中，将其测评结果分为“优秀、合格、不合格”三个等级，其中不小于80分为“优秀”，小于60分为“不合格”，其它为“合格”．
参考公式：K²= $\frac{n {(a d + b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d．
临界值表：
P（K²≥k₀）
0.15
0.10
0.05
0.025
0.010
k₀
2.072
2.706
3.841
5.024
6.635

(1)、某校高一年级有男生500人，女生400人，为了解性别对该综合素质评价结果的影响，采用分层抽样的方法从高一学生中抽取45名学生的综合素质评价结果，其各个等级的频数统计如下表：
等级
优秀
合格
不合格
男生（人）
15
x
5
女生（人）
15
3
y
根据表中统计的数据填写下面2×2列联表，并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”？
优秀
男生
女生
总计
非优秀
总计

(2)、以（1）中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率，且每名学生是否“优秀”相互独立，现从该市高一学生中随机抽取3人．
①求所选3人中恰有2人综合素质评价为“优秀”的概率；
②记X表示这3人中综合素质评价等级为“优秀”的个数，求X的数学期望．

查看试题解析
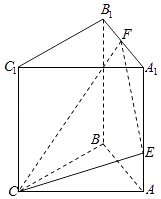
19. 在三棱柱ABC﹣A₁B₁C₁中，CA=CB，侧面ABB₁A₁是边长为2的正方形，点E，F分别在线段AA₁、A₁B₁上，且AE= $\frac{1}{2}$ ，A₁F= $\frac{3}{4}$ ，CE⊥EF．
（Ⅰ）证明：平面ABB₁A₁⊥平面ABC；
（Ⅱ）若CA⊥CB，求直线AC₁与平面CEF所成角的正弦值．

查看试题解析
20. 过抛物线C：y²=2px（p＞0）的焦点F的直线交抛物线于A，B两点，且A，B两点的纵坐标之积为﹣4．

(1)、求抛物线C的方程；

(2)、已知点D的坐标为（4，0），若过D和B两点的直线交抛物线C的准线于P点，求证：直线AP与x轴交于一定点．

查看试题解析
21. 已知函数f（x）= $\frac{a x^{2}}{e^{x}}$ ，直线y= $\frac{1}{e}$ x为曲线y=f（x）的切线（e为自然对数的底数）．

(1)、求实数a的值；

(2)、用min{m，n}表示m，n中的最小值，设函数g（x）=min{f（x），x﹣ $\frac{1}{x}$ }（x＞0），若函数h（x）=g（x）﹣cx²为增函数，求实数c的取值范围．

查看试题解析
22. 如图，AB为圆O的直径，C在圆O上，CF⊥AB于F，点D为线段CF上任意一点，延长AD交圆O于E，∠AEC=30°．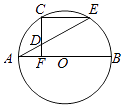

(1)、求证：AF=FO；

(2)、若CF= $\sqrt{3}$ ，求AD•AE的值．

查看试题解析
23. 已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合，若曲线C的参数方程为 ${\begin{cases} x = 3 + 2 \cos α \\ y = 2 \sin α \end{cases}$ （α是参数），直线l的极坐标方程为 $\sqrt{2}$ ρsin（θ﹣ $\frac{π}{4}$ ）=1．

(1)、将曲线C的参数方程化为极坐标方程；

(2)、由直线l上一点向曲线C引切线，求切线长的最小值．

查看试题解析
24. 已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解，记实数m的最大值为M．

(1)、求M的值；

(2)、正数a，b，c满足a+2b+c=M，求证： $\frac{1}{a + b}$ + $\frac{1}{b + c}$ ≥1．

查看试题解析

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010
k₀	2.072	2.706	3.841	5.024	6.635

等级	优秀	合格	不合格
男生（人）	15	x	5
女生（人）	15	3	y

优秀	男生	女生	总计
非优秀
总计