2014年海南省中考数学试卷
试卷更新日期:2017-05-18 类型:中考真卷
一、选择题
-
1. 5的相反数是( )A、 B、﹣5 C、±5 D、﹣2. 方程x+2=1的解是( )A、3 B、﹣3 C、1 D、﹣13. 据报道,我省西环高铁预计2015年底建成通车,计划总投资27100000000元,数据27100000000用科学记数法表示为( )A、271×108 B、2.71×109 C、2.71×1010 D、2.71×10114. 一组数据:﹣2,1,1,0,2,1,则这组数据的众数是( )A、﹣2 B、0 C、1 D、25. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )A、120° B、90° C、60° D、30°7. 如图,已知AB∥CD,与∠1是同位角的角是( )
6. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )A、120° B、90° C、60° D、30°7. 如图,已知AB∥CD,与∠1是同位角的角是( ) A、∠2 B、∠3 C、∠4 D、∠58. 如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( )
A、∠2 B、∠3 C、∠4 D、∠58. 如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6),B(﹣6,2),E(2,1),则点D的坐标为( ) A、(﹣4,6) B、(4,6) C、(﹣2,1) D、(6,2)9. 下列式子从左到右变形是因式分解的是( )A、a2+4a﹣21=a(a+4)﹣21 B、a2+4a﹣21=(a﹣3)(a+7) C、(a﹣3)(a+7)=a2+4a﹣21 D、a2+4a﹣21=(a+2)2﹣2510. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )A、100(1+x)2=81 B、100(1﹣x)2=81 C、100(1﹣x%)2=81 D、100x2=8111. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、 cm B、 cm C、3cm D、 cm12. 一个不透明的袋子中有3个分别标有3,1,﹣2的球,这些球除了所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之和为负数的概率是( )A、 B、 C、 D、13. 将抛物线y=x2平移得到抛物线y=(x+2)2 , 则这个平移过程正确的是( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位14. 已知k1>0>k2 , 则函数y=k1x和y= 的图象在同一平面直角坐标系中大致是( )A、
A、(﹣4,6) B、(4,6) C、(﹣2,1) D、(6,2)9. 下列式子从左到右变形是因式分解的是( )A、a2+4a﹣21=a(a+4)﹣21 B、a2+4a﹣21=(a﹣3)(a+7) C、(a﹣3)(a+7)=a2+4a﹣21 D、a2+4a﹣21=(a+2)2﹣2510. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )A、100(1+x)2=81 B、100(1﹣x)2=81 C、100(1﹣x%)2=81 D、100x2=8111. 一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )A、 cm B、 cm C、3cm D、 cm12. 一个不透明的袋子中有3个分别标有3,1,﹣2的球,这些球除了所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之和为负数的概率是( )A、 B、 C、 D、13. 将抛物线y=x2平移得到抛物线y=(x+2)2 , 则这个平移过程正确的是( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位14. 已知k1>0>k2 , 则函数y=k1x和y= 的图象在同一平面直角坐标系中大致是( )A、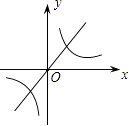 B、
B、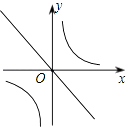 C、
C、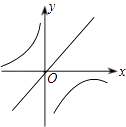 D、
D、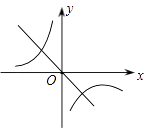
二、填空题
-
15. 购买单价为a元的笔记本3本和单价为b元的铅笔5支应付款元.16. 函数 中,自变量x的取值范围是 .17. 如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 ,AC=5,AD=4,则⊙O的直径AE= .
 18. 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是
18. 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是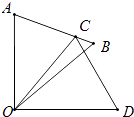
三、解答题
-
19. 计算:(1)、12×(﹣ )+8×2﹣2﹣(﹣1)2(2)、解不等式 ≤ ,并求出它的正整数解.20. 海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们整理的不完整的统计图:

根据以上信息完成下列问题:
(1)、请将条形统计图补充完整;(2)、随机调查的游客有人;在扇形统计图中,A部分所占的圆心角是度;(3)、请根据调查结果估计在1500名游客中喜爱攀锦的约有人.21. 海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元,李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?22. 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: ≈1.414, ≈1.732, ≈2.236)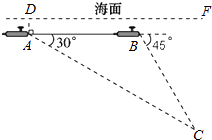 23. 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC于点E,F,作BH⊥AF于点H,分别交AC,CD于点G,P,连接GE,GF.
23. 如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD,BC于点E,F,作BH⊥AF于点H,分别交AC,CD于点G,P,连接GE,GF.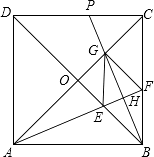 (1)、求证:△OAE≌△OBG;(2)、试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;(3)、试求: 的值(结果保留根号).24. 如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)、求证:△OAE≌△OBG;(2)、试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由;(3)、试求: 的值(结果保留根号).24. 如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点. (1)、求此抛物线的解析式;(2)、当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
(1)、求此抛物线的解析式;(2)、当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.