2012年江苏省南通市中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入出卷网下载

一、选择题

1. 计算6÷（﹣3）的结果是（）

A、﹣ $\frac{1}{2}$ B、﹣2 C、﹣3 D、﹣18

查看试题解析
2. 计算（﹣x²）•x³的结果是（）

A、x³ B、﹣x⁵ C、x⁶ D、﹣x⁶

查看试题解析
3. 已知∠a=32°，则∠a的补角为（）

A、58° B、68° C、148° D、168°

查看试题解析
4. 至2011年末，南通市户籍人口为764.88万人，将764.88万用科学记数法表示为（）

A、7.6488×10⁴ B、7.6488×10⁵ C、7.6488×10⁶ D、7.6488×10⁷

查看试题解析
5.
线段MN在直角坐标系中的位置如图所示，若线段M′N′与MN关于y轴对称，则点M的对应点M′的坐标为（）

A、（4，2） B、（﹣4，2） C、（﹣4，﹣2） D、（4，﹣2）

查看试题解析
6. 已知x²+16x+k是完全平方式，则常数k等于（）

A、64 B、48 C、32 D、16

查看试题解析
7. 如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（）

A、360° B、250° C、180° D、140°

查看试题解析
8. 如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为（）

A、 $\sqrt{3}$ cm B、2cm C、2 $\sqrt{3}$ cm D、4cm

查看试题解析
9. 已知A（﹣1，y₁），B（2，y₂）两点在双曲线y= $\frac{3 + 2 m}{x}$ 上，且 y₁＞y₂ ，则m的取值范围是（）

A、m＜0 B、m＞0 C、m＞﹣ $\frac{3}{2}$ D、m＜﹣ $\frac{3}{2}$

查看试题解析
10. 如图Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，且AC在直线l上，将△ABC绕点A顺时针旋转到①，可得到点P₁ ，此时AP₁=2；将位置①的三角形绕点P₁顺时针旋转到位置②，可得到点P₂ ，此时AP₂=2+ $\sqrt{3}$ ；将位置②的三角形绕点P₂顺时针旋转到位置③，可得到点P₃ ，此时AP₃=3+ $\sqrt{3}$ ；…按此规律继续旋转，直到点P₂₀₁₂为止，则AP₂₀₁₂等于（）

A、2011+671 $\sqrt{3}$ B、2012+671 $\sqrt{3}$ C、2013+671 $\sqrt{3}$ D、2014+671 $\sqrt{3}$

查看试题解析

二、填空题

11. 单项式3x²y的系数为

查看试题解析
12. 函数y= $\frac{1}{x - 5}$ 中，自变量x的取值范围是

查看试题解析
13. 某校9名同学的身高（单位：cm）分别是：163，165，167，164，165，166，165，164，166，则这组数据的众数为．

查看试题解析
14. 如图，⊙O中，∠AOB=46°，则∠ACB=度．

查看试题解析
15. 甲种电影票每张20元，乙种电影票每张15元，若购买甲、乙两种电影票共40张，恰好用去700元，则甲种电影票买了张．

查看试题解析
16. 如图，梯形ABCD中，AB∥DC，∠A+∠B=90°，AB=7cm，BC=3cm，AD=4cm，则CD=cm．

查看试题解析
17. 设α，β是一元二次方程x²+3x﹣7=0的两个根，则α²+4α+β= ．

查看试题解析
18. 无论a取什么实数，点P（a﹣1，2a﹣3）都在直线l上．Q（m，n）是直线l上的点，则（2m﹣n+3）²的值等于．

查看试题解析

三、三.解答题

19. 计算：

(1)、|﹣1|+（﹣2）²+（7﹣π）⁰﹣（ $\frac{1}{3}$ ）^﹣¹

(2)、 $\sqrt{48}$ ÷ $\sqrt{3}$ ﹣ $\sqrt{\frac{1}{2}}$ × $\sqrt{12}$ + $\sqrt{24}$ ．

查看试题解析
20. 先化简，再求值： $[1 + \frac{2 x - 4}{(x + 1) (x - 2)}] \div \frac{x + 3}{x^{2} - 1}$ ，其中x=6．

查看试题解析
21. 为了了解学生参加家务劳动的情况，某中学随机抽取部分学生，统计他们双休日两天家务劳动的时间，将统计的劳动时间（单位：分钟）分成5组：30≤x＜60，60≤x＜90，90≤x＜120，120≤x＜150，150≤x＜180，绘制成频数分布直方图．请根据图中提供的信息，解答下列问题：

(1)、这次抽样调查的样本容量是；

(2)、根据小组60≤x＜90的组中值75，估计该组中所有数据的和为；

(3)、该中学共有1000名学生，估计双休日两天有多少名学生家务劳动的时间不小于90分钟？

查看试题解析
22. 如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离．

查看试题解析
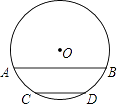23.
如图，某测量船位于海岛P的北偏西60°方向，距离海岛100海里的A处，它沿正南方向航行一段时间后，到达位于海岛P的西南方向上的B处，求测量船从A处航行到B处的路程（结果保留根号）．

查看试题解析
24. 四张扑克牌的点数分别是2，3，4，8，将它们洗匀后背面朝上放在桌上．

(1)、从中随机抽取一张牌，求这张牌的点数是偶数的概率；

(2)、从中随机抽取一张牌，接着再抽取一张，求这两张牌的点数都是偶数的概率．

查看试题解析
25. 甲、乙两地距离300km，一辆货车和一辆轿车先后从甲地出发驶向乙地．如图，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系，根据图象，解答下列问题：

(1)、线段CD表示轿车在途中停留了 h；

(2)、求线段DE对应的函数解析式；

(3)、求轿车从甲地出发后经过多长时间追上货车．

查看试题解析
26. 菱形ABCD中，∠B=60°，点E在边BC上，点F在边CD上．

(1)、如图1，若E是BC的中点，∠AEF=60°，求证：BE=DF；

(2)、如图2，若∠EAF=60°，求证：△AEF是等边三角形．

查看试题解析
27. 如图△ABC中，AB=AC=10厘米，BC=12厘米，D是BC的中点，点P从B出发，以a厘米/秒（a＞0）的速度沿BA匀速向点A运动，点Q同时以1厘米/秒的速度从D出发，沿DB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为t秒．

(1)、若a=2，△BPQ∽△BDA，求t的值；

(2)、设点M在AC上，四边形PQCM为平行四边形．
①若a= $\frac{5}{2}$ ，求PQ的长；
②是否存在实数a，使得点P在∠ACB的平分线上？若存在，请求出a的值；若不存在，请说明理由．

查看试题解析
28.
如图，经过点A（0，﹣4）的抛物线y= $\frac{1}{2}$ x²+bx+c与x轴相交于B（﹣2，0），C两点，O为坐标原点．

(1)、求抛物线的解析式；

(2)、将抛物线y= $\frac{1}{2}$ x²+bx+c向上平移 $\frac{7}{2}$ 个单位长度，再向左平移m（m＞0）个单位长度得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；

(3)、设点M在y轴上，∠OMB+∠OAB=∠ACB，求AM的长．

查看试题解析