2012年江苏省淮安市中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入 出卷网 下载

一、选择题

  • 1. 12 的相反数是（   ）

    A、﹣ 12 B、12 C、﹣2 D、2

    查看试题解析

  • 2. 下列图形中，是中心对称图形的是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 3. 下列运算正确的是（   ）
    A、a2•a3=a6 B、a3÷a2=a C、（a3）2=a9 D、a2+a3=a5

    查看试题解析

  • 4. 如图，AB是⊙O的直径，点C在⊙O上，若∠A=40°，则∠B的度数为（    ）

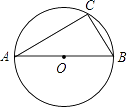    A、80° B、60° C、50° D、40°

    查看试题解析

  • 5.

    如图所示的几何体的俯视图是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 6. 已知反比例函数y= m−1x 的图象如图所示，则实数m的取值范围是（   ）

    A、m＞1 B、m＞0 C、m＜1 D、m＜0

    查看试题解析

  • 7. 方程x2﹣3x=0的解为（   ）

    A、x=0 B、x=3 C、x1=0，x2=﹣3 D、x1=0，x2=3

    查看试题解析

  • 8. 下列说法正确的是（   ）
    A、两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定 B、某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生 C、学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大 D、为了解我是学校“阳光体育”活动开展情况，必须采用普查的方式

    查看试题解析

二、填空题

  • 9. |﹣3|= ．

    查看试题解析

  • 10. 2011年淮安市人均GDP约为35200元，35200用科学记数法表示为

    查看试题解析

  • 11. 数据1，3，2，1，4的中位数是 ．

    查看试题解析

  • 12. 分解因式：a2+2a+1= ．

    查看试题解析

  • 13. 菱形ABCD中，若对角线长AC=8cm，BD=6cm，则边长AB=cm．

    查看试题解析

  • 14. 如图，△ABC中，AB=AC，AD⊥BC，垂足为D，若∠BAC=70°，则∠BAD=°．

    查看试题解析

  • 15. 如图，⊙M与⊙N外切，MN=10cm，若⊙M的半径为6cm，则⊙N的半径为 cm．

    查看试题解析

  • 16. 若 5 的值在两个整数a与a+1之间，则a= ．

    查看试题解析

  • 17. 若圆锥的底面半径为2cm，母线长为5cm，则此圆锥的侧面积是 cm2 ．

    查看试题解析

  • 18. 如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差 km/h．

    查看试题解析

三、解答题

  • 19. 计算：
    (1)、22﹣20120+（﹣6）÷3；
    (2)、x2−1x⋅xx+1+(3x+1) ．

    查看试题解析

  • 20. 解不等式组： {x−1>03(x+2)<5x ．

    查看试题解析

  • 21. 已知：如图，在▱ABCD中，延长AB到点E，使BE=AB，连接DE交BC于点F．求证：△BEF≌△CDF．

    查看试题解析

  • 22. 有一个渔具包，包内装有A，B两只鱼竿，长度分别为3.6m，4.5m，包内还装有绑好鱼钩的a1 ， a2 ， b三根钓鱼线，长度分别为3.6m，3.6m，4.5m．若从包内随即取出一支鱼竿，再随即取出一根钓鱼线，则鱼竿和鱼钩线长度相同的概率是多少？（请画树状图或列表说明）

    查看试题解析

  • 23. 实施“节能产品惠民工程”一年半以来，国家通过发放补贴的形式支持推广高效节能空调、1.6升及以下排量节能汽车、节能灯三类产品，其中推广节能汽车约120万辆，按每辆3000元标准给予一次性定额补贴．小刚同学根据了解到的信息进行统计分析，绘制出两幅不完整的统计图：

    （注：图中A表示“高效节能空调”；B表示“1.6升及以下排量节能汽车”；C表示“节能灯”）

    (1)、国家对上述三类产品共发放补贴金额亿元，“B”所在扇形的圆心角为°；
    (2)、补全条形统计图；
    (3)、国家计划再拿出98亿元继续推广上述三类产品．请你预测，可再推广节能汽车多少万辆？

    查看试题解析

  • 24. 如图，△ABC中，∠C=90°，点D在AC上，已知∠BDC=45°，BD=10 2 ，AB=20．求∠A的度数．

    查看试题解析

  • 25. 某省公布的居民用电阶梯电价听证方案如下：

    第一档电量

    第二档电量

    第三档电量

    月用电量210度以下，每度价格0.52元

    月用电量210度至350度，每度比第一档提价0.05元

    月用电量350度以上，每度比第一档提价0.30元

    例：若某户月用电量400度，则需交电费为210×0.52+（350﹣210）×（0.52+0.05）+（400﹣350）×（0.52+0.30）=230（元）

    (1)、如果按此方案计算，小华家5月份的电费为138.84元，请你求出小华家5月份的用电量；
    (2)、以此方案请你回答：若小华家某月的电费为a元，则小华家该月用电量属于第几档？

    查看试题解析

  • 26. 国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴120元．种粮大户老王今年种了150亩地，计划明年再承租50～150亩土地种粮以增加收入，考虑各种因素，预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系如图所示：

    (1)、今年老王种粮可获得补贴多少元？
    (2)、根据图象，求y与x之间的函数关系式；
    (3)、若明年每亩的售粮收入能达到2140元，求老王明年种粮总收入W（元）与种粮面积x（亩）之间的函数关系式．当种粮面积为多少亩时，总收入最高？并求出最高总收入．

    查看试题解析

  • 27. 如图，矩形OABC在平面直角坐标系中，O为坐标原点，点A（0，4），C（2，0）．将矩形OABC绕点O按顺时针方向旋转135°，得到矩形EFGH（点E与O重合）．

    (1)、若GH交y轴于点M，则∠FOM=°，OM=；
    (2)、将矩形EFGH沿y轴向上平移t个单位．

    ①直线GH与x轴交于点D，若AD∥BO，求t的值；

    ②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位，试求当0＜t≤4 2 ﹣2时，S与t之间的函数关系式．

    查看试题解析

  • 28. 阅读理解

    如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．

    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．

    探究发现

    (1)、△ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？（填“是”或“不是”）．
    (2)、小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为

    应用提升

    (3)、小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．

    请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

    查看试题解析