2012年海南省中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 计算x²•x³ ，正确结果是（）

A、x⁶ B、x⁵ C、x⁹ D、x⁸

查看试题解析
3. 当x=﹣2时，代数式x+3的值是（）

A、1 B、﹣1 C、5 D、﹣5

查看试题解析
4. 如图竖直放置的圆柱体的俯视图是（）

A、长方形 B、正方形 C、圆 D、等腰梯形

查看试题解析
5. 一个三角形的两边长分别为3cm和7cm，则此三角形的第三边的长可能是（）

A、3cm B、4cm C、7cm D、11cm

查看试题解析
6. 连接海口、文昌两市的跨海大桥﹣﹣铺前大桥，近日获国家发改委批准建设，该桥估计总投资约为1460000000元，数据1460000000用科学记数法表示应是（）

A、1.46×10⁷ B、1.46×10⁹ C、1.46×10¹⁰ D、0.146×10¹⁰

查看试题解析
7. 要从小强、小红和小华三人中随机选两人作为旗手，则小强和小红同时入选的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析
8. 分式方程 $\frac{1}{x - 1} + \frac{2 x}{x + 1}$ =2的解是（）

A、1 B、﹣1 C、3 D、无解

查看试题解析
9. 如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD相交于点O，且AB≠AD，则下列判断不正确的是（）

A、△ABD≌△CBD B、△ABC≌△ADC C、△AOB≌△COB D、△AOD≌△COD

查看试题解析
10. 如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（）

A、∠ABD=∠C B、∠ADB=∠ABC C、 $\frac{A B}{B D} = \frac{C B}{C D}$ D、 $\frac{A D}{A B} = \frac{A B}{A C}$

查看试题解析
11. 如图，正比例函数y=k₁x与反比例函数y= $\frac{k_{2}}{x}$ 的图象相交于A、B两点，若点A的坐标为（2，1），则点B的坐标是（）

A、（1，2） B、（﹣2，1） C、（﹣1，﹣2） D、（﹣2，﹣1）

查看试题解析
12. 小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n上，测得∠α=120°，则∠β的度数是（）

A、45° B、55° C、65° D、75°

查看试题解析
13. 如图，点A、B、O是正方形网格上的三个格点，⊙O的半径是OA，点P是优弧 $\hat{A m B}$ 上的一点，则tan∠APB的值是（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
14. 星期六，小亮从家里骑自行车到同学家去玩，然后返回，图是他离家的路程y（千米）与时间x（分钟）的函数图象，根据图象信息，下列说法不一定正确的是（）

A、小亮到同学家的路程是3千米 B、小亮在同学家逗留的时间是1小时 C、小亮去时走上坡路，回家时走下坡路 D、小亮回家时用的时间比去时用的时间少

查看试题解析

二、填空题

15. 分解因式：x²﹣1= ．

查看试题解析
16. 农民张大伯因病住院，手术费用为a元，其他费用为b元，由于参加农村合作医疗，手术费用报销85%，其他费用报销60%，则张大伯此住院可报销元（用代数式表示）．

查看试题解析
17. 如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是．

查看试题解析
18. 如图，∠APB=30°，圆心在PB上的⊙O的半径为1cm，OP=3cm，若⊙O沿BP方向平移，当⊙O与PA相切时，圆心O平移的距离为 cm．

查看试题解析

三、解答题

19. 计算题

(1)、计算： $\sqrt{8}$ + $\sqrt{2}$ +|﹣4|﹣（ $\frac{1}{3}$ ）^﹣¹

(2)、解不等式组： ${\begin{matrix} x - 1 < 3 \\ 3 - x > 0 \end{matrix}$ ．

查看试题解析
20. 为了进一步推进海南国际旅游岛建设，海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》，第八条规定：“旅行社引进会议规模达到200人以上，入住本市A类旅游饭店，每次会议奖励2万元；入住本市B类旅游饭店，每次会议奖励1万元．”某旅行社5月份引进符合奖励规定的会议共18次，得到28万元奖金，求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次？

查看试题解析
21. 某校有学生2100人，在“文明我先行”活动中，开设了“法律、礼仪、环保、感恩、互助”五门校本课程，规定每位学生必须且只能选一门，为了解学生的报名意向，学校随机调查了100名学生，并制成统计表：校本课程意向统计表
课程类型
频数
频率（%）
法律
s
0.08
礼仪
a
0.20
环保
27
0.27
感恩
b
m
互助
15
0.15
合计
100
1.00
请根据统计表的信息，解答下列问题；

(1)、在这次调查活动中，学校采取的调查方式是（填写“普查”或“抽样调查”）；

(2)、a= ， b= ， m=；

(3)、如果要画“校本课程报名意向扇形统计图”，那么“礼仪”类校本课程对应的扇形圆心角的度数是；

(4)、请你估计，选择“感恩”类校本课程的学生约有人．

查看试题解析
22.
如图，在正方形网格中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（﹣2，4）、（﹣2，0）、（﹣4，1），结合所给的平面直角坐标系解答下列问题：

(1)、画出△ABC关于原点O对称的△A₁B₁C₁；

(2)、平移△ABC，使点A移到点A₂（0，2），画出平移后△A₂B₂C₂并写出点B₂、C₂的坐标；

(3)、在△ABC、△A₁B₁C₁、△A₂B₂C₂中，△A₂B₂C₂与成中心对称，其对称中心坐标为．

查看试题解析
23. 如图（1），在矩形ABCD中，把∠B、∠D分别翻折，使点B、D恰好落在对角线AC上的点E、F处，折痕分别为CM、AN，

(1)、求证：△ADN≌△CBM；

(2)、请连接MF、NE，证明四边形MFNE是平行四边形；四边形MFNE是菱形吗？请说明理由；

(3)、点P、Q是矩形的边CD、AB上的两点，连接PQ、CQ、MN，如图（2）所示，若PQ=CQ，PQ∥MN，且AB=4cm，BC=3cm，求PC的长度．

查看试题解析
24.
如图，顶点为P（4，﹣4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，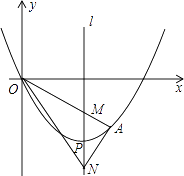

(1)、求该二次函数的关系式；

(2)、若点A的坐标是（6，﹣3），求△ANO的面积；

(3)、若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：
①证明：∠ANM=∠ONM；
②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．

查看试题解析

课程类型	频数	频率（%）
法律	s	0.08
礼仪	a	0.20
环保	27	0.27
感恩	b	m
互助	15	0.15
合计	100	1.00