2011年海南省中考数学试卷
试卷更新日期：2017-05-18 类型：中考真卷
一、选择题
-
1. ﹣3的绝对值是（ ）A、﹣3 B、3 C、- D、2. 计算（a2）3 ， 正确结果是（ ）A、a5 B、a6 C、a8 D、a93. 不等式x﹣2＜0的解集是（ ）A、x＞﹣2 B、x＜﹣2 C、x＞2 D、x＜24. 数据2，﹣l，0，1，2的中位数是（ ）A、1 B、0 C、﹣1 D、25. “比a的2倍大1的数”用代数式表示是（ ）A、2（a+1） B、2（a﹣1） C、2a+1 D、2a﹣16. 如图所示几何体的俯枧图是（ ）
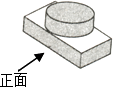A、
B、
C、
D、
7. 正方形是轴对称图形，它的对称轴共有（ ）A、1条 B、2条 C、3条 D、4条8. 一枚质地均匀的普通硬币重复掷两次，落地后两次都是正面朝上的概率是（ ）A、1 B、 C、 D、9. 海南省2010年第六次人口普查数据显示，2010年11月1日零时．全省总人口为8671518人．数据8671518用科学记数法（保留三个有效数字）表示应是（ ）A、8.7×106 B、8.7×107 C、8.67×106 D、8.67×10710. 已知点A（2，3）在反比例函数 的图象上，则k的值是（ ）A、﹣7 B、7 C、﹣5 D、511. 如图．已知直线a，b被直线c所截，且a∥b，∠1=48°，那么∠2的度数为（ ）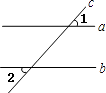
A、42° B、48° C、52° D、132°12. 如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，则图中相似三角形共有（ ）
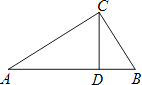A、1对 B、2对 C、3对 D、4对13. 如图，在以AB为直径的半圆O中，C是它的中点，若AC=2，则△ABC的面积是（ ）
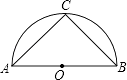A、1.5 B、2 C、3 D、414. 如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是（ ）
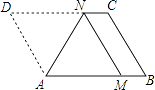A、①②都对 B、①②都错 C、①对②错 D、①错②对二、填空题
-
15. 分解因式：x2﹣4= ．16. 方程 的解是 ．17. 如图，在△ABC中，AB=AC=3cm，AB的垂直平分线交AC于点N，△BCN的周长是5cm，则BC的长等于 cm．
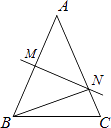18. 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，连接BC交⊙O于点D，若∠C=50°，则∠AOD=
三、解答题
-
19. 计算(1)、(2)、（a+1）2﹣a（a﹣1）20. 第十六届亚远会共颁发金牌477枚，如图是不完整的金牌数条形统计图和扇形统计图，
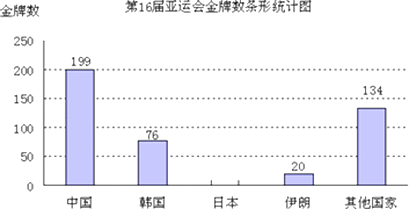
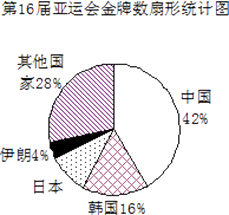
根据以上信息．觯答下列问题：
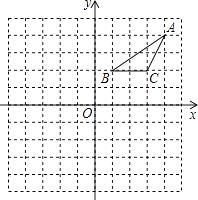
(1)、请将条形统计图补充完整；(2)、中国体育健儿在第十六届亚运会上共夺得金牌枚；(3)、在扇形统计图中，日本代表团所对应的扇形的圆心角约为°（精确到1°）．21. 在正方形网格中建立如图所示的平面直角坐标系xOy．△ABC的三个顶点都在格点上，点A的坐标是（4，4 ），请解答下列问题：(1)、将△ABC向下平移5个单位长度，画出平移后的A1B1C1 ， 并写出点A的对应点A1的坐标；(2)、画出△A1B1C1关于y轴对称的△A2B2C2；(3)、将△ABC绕点C逆时针旋转90°，画出旋转后的△A3B3C．
22. 在海南东环高铁上运行的一列“和谐号”动车组有一等车厢和二等车厢共6节，一共设有座位496个．其中每节一等车厢设座位64个，每节二等车厢设座位92个．试求该列车一等车厢和二等车厢各有多少节？23. 如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．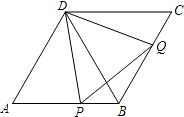
(1)、求证：△BDQ≌△ADP；(2)、已知AD=3，AP=2，求cos∠BPQ的值（结果保留根号）．24.如图，已知抛物线y=﹣x2+bx+9﹣b2（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．
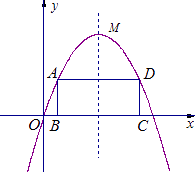(1)、求该抛物线所对应的函数关系式；(2)、设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B，DC⊥x轴于点C．①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；
②求矩形ABCD的周长的最大值，并写出此时点A的坐标；
③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断并说明理由．