广东省深圳市南山区育才二中2018-2019学年中考数学一模试卷
试卷更新日期:2019-05-10 类型:中考模拟
一、选择题(本题共12小题,每小题3分,共36分.)
-
1. 的相反数是( )A、2 B、﹣2 C、 D、﹣2. 下列图形既是轴对称图形也是中心对称图形的是( )A、
 B、
B、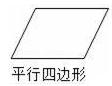 C、
C、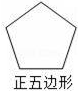 D、
D、 3. 港珠澳大桥2018年10月23日正式开通,整个大桥造价超过720亿元人民币,是连接香港、珠海、澳门的超大型跨海通道.数据“720亿”用科学记数法表示为( )A、0.72×1011 B、7.2×1011 C、7.2×1010 D、72×1094. 如图所示的几何体,它的俯视图是( )
3. 港珠澳大桥2018年10月23日正式开通,整个大桥造价超过720亿元人民币,是连接香港、珠海、澳门的超大型跨海通道.数据“720亿”用科学记数法表示为( )A、0.72×1011 B、7.2×1011 C、7.2×1010 D、72×1094. 如图所示的几何体,它的俯视图是( )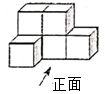 A、
A、 B、
B、 C、
C、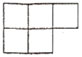 D、
D、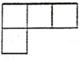 5. 下列说法正确的是( )A、“明天降雨的概率为50%”,意味着明天一定有半天都在降雨 B、了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式 C、掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件 D、一组数据的方差越大,则这组数据的波动也越大6. 下列计算正确的是( )A、x4+x2=x6 B、(﹣m)7÷(﹣m)2=﹣m5 C、(3x2y)2=6x4y2 D、(a+b)2=a2+b27. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
5. 下列说法正确的是( )A、“明天降雨的概率为50%”,意味着明天一定有半天都在降雨 B、了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式 C、掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件 D、一组数据的方差越大,则这组数据的波动也越大6. 下列计算正确的是( )A、x4+x2=x6 B、(﹣m)7÷(﹣m)2=﹣m5 C、(3x2y)2=6x4y2 D、(a+b)2=a2+b27. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )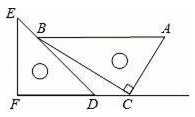 A、10° B、15° C、18° D、30°8. 把不等式组的解集表示在数轴上,下列选项正确的是( )
A、10° B、15° C、18° D、30°8. 把不等式组的解集表示在数轴上,下列选项正确的是( )
A、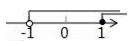 B、
B、 C、
C、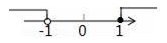 D、
D、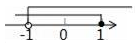 9. 为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,求学校购买甲、乙两种花木各多少棵?设购买甲种花木x棵、乙种花木y棵,根据题意列出的方程组正确的是( )A、 B、 C、 D、10. 对于反比例函数y=﹣ ,下列说法错误的是( )A、图象分布在第二、四象限 B、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y2 C、图象经过点(1,﹣2) D、当x>0时,y随x的增大而增大11. 如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )
9. 为了美化校园,学校计划购买甲、乙两种花木共200棵进行绿化,其中甲种花木每棵80元,乙种花木每棵100元,若购买甲、乙两种花木共花费17600元,求学校购买甲、乙两种花木各多少棵?设购买甲种花木x棵、乙种花木y棵,根据题意列出的方程组正确的是( )A、 B、 C、 D、10. 对于反比例函数y=﹣ ,下列说法错误的是( )A、图象分布在第二、四象限 B、若点A(x1 , y1),B(x2 , y2)都在图象上,且x1<x2 , 则y1<y2 C、图象经过点(1,﹣2) D、当x>0时,y随x的增大而增大11. 如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为( )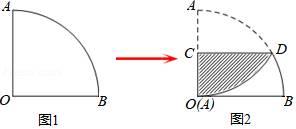 A、 B、 C、 D、12. 如图,等边三角形ABC的边长为4,点O是△ABC的内心,∠FOG=120”,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE:②S△ODE=S△BDE:③四边形ODBE的面积始终等于 ;④△BDE周长的最小值为6.
A、 B、 C、 D、12. 如图,等边三角形ABC的边长为4,点O是△ABC的内心,∠FOG=120”,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE:②S△ODE=S△BDE:③四边形ODBE的面积始终等于 ;④△BDE周长的最小值为6.上述结论中正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(共12分)
-
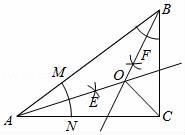
13. 分解因式:xy2﹣9x= .14. 在一个不透明的袋子里,装有除颜色外完全相同的2个黑球和1个红球,现从袋子中随机摸出两个球,则摸到1个黑球和1个红球的概率是 .15. 若x是不等于1的实数,我们把 称为x的差倒数,如2的差倒数是 ,﹣1的差倒数为 ,现已知 ,x2是x1的倒差数,x3是x2的倒差数,x4是x3的倒差数,…,依此类推,则x2019=16. 如图,在△ABC中,AB=13,AC=12,BC=5,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB、AC于点M、N;②分别以点M、N为圆心,以大于 MN的长为半径作弧,两弧相交于点E;③作射线AE;④以同样的方法作射线BF,AE交BF于点O,连接OC,则OC=
三、解答题(共52分)
-
17. 计算18. 先化简 ,然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值。19. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
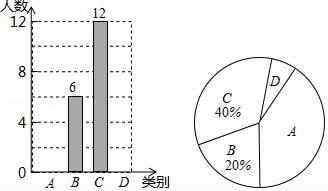
请依据统计结果回答下列问题:
(1)、本次调查中,一共调查了位好友.(2)、已知A类好友人数是D类好友人数的5倍.①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 ▲ 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
20. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.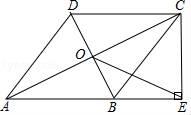 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.21. 随着生活水平的提高,人们对饮水品质的需求越来越高,深圳市某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等,(1)、求每台A型、B型净水器的进价各是多少元?(2)、该公司计划购进A,B两种型号的净水器共55台进行试销,其中A型净水器为m台,购买两种净水器的总资金不超过10.8万元.试销时A型净水器每台售价2500元,B型净水器每台售价2180元,该公司决定从销售A型净水器的利润中按每台捐献a(70<a<80)元作为公司帮扶贫困村饮水改造资金,设该公司售完55台净水器并捐献扶贫资金后获得的利润为W元,求W的最大值.22. 如图所示,⊙O的半径为5,点A是⊙O上一点,直线l过点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD的延长线交直线l于点F,点A是 的中点.
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.21. 随着生活水平的提高,人们对饮水品质的需求越来越高,深圳市某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等,(1)、求每台A型、B型净水器的进价各是多少元?(2)、该公司计划购进A,B两种型号的净水器共55台进行试销,其中A型净水器为m台,购买两种净水器的总资金不超过10.8万元.试销时A型净水器每台售价2500元,B型净水器每台售价2180元,该公司决定从销售A型净水器的利润中按每台捐献a(70<a<80)元作为公司帮扶贫困村饮水改造资金,设该公司售完55台净水器并捐献扶贫资金后获得的利润为W元,求W的最大值.22. 如图所示,⊙O的半径为5,点A是⊙O上一点,直线l过点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD的延长线交直线l于点F,点A是 的中点.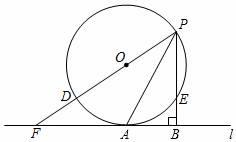 (1)、求证:直线l是⊙O的切线;(2)、若PA=8,求PB的长.23. 如图1,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y= x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数图象上.
(1)、求证:直线l是⊙O的切线;(2)、若PA=8,求PB的长.23. 如图1,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y= x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数图象上. (1)、求此二次函数的表达式;(2)、如图1,连接PC,PB,设△PCB的面积为S,求S的最大值;(3)、如图2,过点P作PM⊥BC于点M,是否存在点P,使得△CPM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点P的横坐标;若不存在,请说明理由.
(1)、求此二次函数的表达式;(2)、如图1,连接PC,PB,设△PCB的面积为S,求S的最大值;(3)、如图2,过点P作PM⊥BC于点M,是否存在点P,使得△CPM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点P的横坐标;若不存在,请说明理由.