2011年江苏省扬州市中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的相反数是（）

A、2 B、 $\frac{1}{2}$ C、﹣2 D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、a²•a³=a⁶ B、（a+b）（a﹣2b）=a²﹣2b² C、（ab³）²=a²b⁶ D、5a﹣2a=3

查看试题解析
3. 下列调査，适合用普査方式的是（）

A、了解一批炮弹的杀伤半径 B、了解扬州电视台《关注》栏目的收视率 C、了解长江中鱼的种类 D、了解某班学生对“扬州精神”的知晓率

查看试题解析
4. 已知相交两圆的半径分別为4和7，则它们的圆心距可能是（）

A、2 B、3 C、6 D、11

查看试题解析
5. 如图是由几个小立方块所搭成的几何体的俯视图，小正方形体的数字表示该位置小立方块的个数，则该几何体的主视图是（）

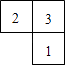A、 B、 C、 D、

查看试题解析
6. 某反比例函数象经过点（﹣1，6），则下列各点中此函数图象也经过的是（）

A、（﹣3，2） B、（3，2） C、（2，3） D、（6，1）

查看试题解析
7. 已知下列命题：①对角线互相平分的四边形是平行四边形；②等腰梯形的对角线相等；③对角线互相垂直的四边形是菱形；④内错角相等．其中假命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在Rt△ABC 中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为（）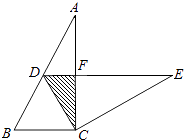

A、30，2 B、60，2 C、60， $\frac{\sqrt{3}}{2}$ D、60， $\sqrt{3}$

查看试题解析

二、填空题

9. “十一五”期间，我市农民收入稳步提高，2010年农民人均纯收人达到9462元．将数据9462用科学记数法表示为．

查看试题解析
10. 化简： $\sqrt{8}$ ﹣ $\sqrt{2}$ = ．

查看试题解析
11. 因式分解：x³﹣4x²+4x= ．

查看试题解析
12. 数学老师布置10道选择题作业，批阅后得到如下统计表．根据表中数据可知，这45名同学答对题数组成的样本的中位数是题．
答对题数
7
8
9
10
人数
4
18
16
7

查看试题解析
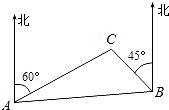
13.
如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则从C点看A、B两岛的视角∠ACB=°．

查看试题解析
14. 某公司4月份的利润为160万元，要使6月份的利润达到250万元，则平均每月增长的百分率是．

查看试题解析
15. 如图，⊙O的弦CD与直径AB相交，若∠BAD=50°，则∠ACD=

查看试题解析
16. 如图，DE是△ABC的中位线，M、N分别是BD、CE的中点，MN=6，则BC= ．

查看试题解析
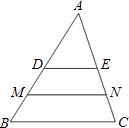17. 如图，已知函数y= $- \frac{3}{x}$ 与y=ax²+bx（a＞0，b＞0）的图象交于点P．点P的纵坐标为1．则关于x的方程ax²+bx+ $\frac{3}{x}$ =0的解为．

查看试题解析
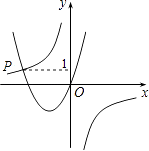18.
如图，立方体的六个面上标着连续的整数，若相对的两个面上所标之数的和相等．则这六个数的和为．

查看试题解析

三、解答题

19. 计算：

(1)、|﹣ $\frac{3}{2}$ |﹣（﹣2011）⁰+4÷（﹣2）³

(2)、 $(1 + \frac{1}{x}) \div \frac{x^{2} - 1}{x}$ ．

查看试题解析
20. 解不等式组 ${\begin{cases} 3 x + 1 < x - 3 \\ \frac{1 + x}{2} \leq \frac{1 + 2 x}{3} + 1 \end{cases}$ ，并写出它的所有整数解．

查看试题解析
21. 为了解某校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成图1和图2两幅尚不完整的统计图．

(1)、本次抽测的男生有人，抽测成绩的众数是；

(2)、请你将图2的统计图补充完整；

(3)、若规定引体向上5次以上（含5次）为体能达标，则该校350名九年级男生中估计有多少人体能达标？

查看试题解析
22. 扬州市体育中考现场考试内容有三项：50米跑为必测项目；另在立定跳远、实心球（二选一）和坐位体前屈、1分钟跳绳（二选一）中选择两项．

(1)、毎位考生有种选择方案；

(2)、用画树状图或列表的方法求小明与小刚选择同种方案的概率．（友情提酲：各种方案用A、B、C、…或①、②、③、…等符号来代表可简化解答过程）

查看试题解析
23. 已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．

(1)、求证：△ABC是等腰三角形；

(2)、判断点O是否在∠BAC的角平分线上，并说明理由．

查看试题解析
24. 古运河是扬州的母亲河．为打造古运河风光带，现有一段长为180米的河道整治任务由A、B两工程队先后接力完成．A工程队每天整治12米，B工程队每天整治8米，共用时20天．

(1)、根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲： ${\begin{cases} x + y = () \\ 12 x + 8 y = () \end{cases}$ ；乙： ${\begin{cases} x + y = () \\ \frac{x}{12} + \frac{y}{8} = () \end{cases}$
根据甲、乙两名问学所列的方程组，请你分别指出未知数x、y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：x表示， y表示；
乙：x表示， y表示．

(2)、求A、B两工程队分别整治河道多少米．（写出完整的解答过程）

查看试题解析
25. 如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=76厘米，∠CED=60°．

(1)、求垂直支架CD的长度；（结果保留根号）

(2)、求水箱半径OD的长度．（结果保留三个有效数字，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.73）

查看试题解析
26. 已知：如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．

(1)、以AB边上一点O为圆心，过A、D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；

(2)、若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=2 $\sqrt{3}$ ，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和π）

查看试题解析
27. 如图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）．现将甲槽中的水匀速注人乙槽，甲、乙两个水槽中水的深度y（厘米）与注水时间x（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：

(1)、图2中折线ABC表示槽中水的深度与注水时间之间的关系，线段DE表示槽中水的深度与注水时间之间的关系（以上两空选塡“甲”或“乙”），点B的纵坐标表示的实际意义是；

(2)、注水多长时间时，甲、乙两个水槽中水的深度相同；

(3)、若乙槽底面积为36平方厘米（壁厚不计），求乙槽中铁块的体积；

(4)、若乙槽中铁块的体积为112立方厘米，求甲槽底面积（壁厚不计）．（直接写成结果）

查看试题解析
28. 在△ABC中，∠BAC=90°，AB＜AC，M是BC边的中点，MN⊥BC交AC于点N．动点P从点B出发沿射线BA以每秒 $\sqrt{3}$ 厘米的速度运动．同时，动点Q从点N出发沿射线NC运动，且始终保持MQ丄MP．设运动时间为t秒（t＞0）．

(1)、△PBM与△QNM相似吗？以图1为例说明理由；

(2)、若∠ABC=60°，AB=4 $\sqrt{3}$ 厘米．
①求动点Q的运动速度；
②设△APQ的面积为S（平方厘米），求S与t的函数关系式．

查看试题解析

答对题数	7	8	9	10
人数	4	18	16	7