2011年江苏省徐州市中考数学试卷

试卷更新日期：2017-05-18 类型：中考真卷

进入出卷网下载

一、选择题

1. 2的相反数是（）

A、﹣2 B、2 C、 $\sqrt{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 2010年我国总人口约为1 370 000 000人，该人口数用科学记数法表示为（）

A、0.137×10¹¹ B、1.37×10⁹ C、13.7×10⁸ D、137×10⁷

查看试题解析
3. 估计 $\sqrt{11}$ 的值（）

A、在2到3之间 B、在3到4之间 C、在4到5之间 D、在5到6之间

查看试题解析
4. 下列运算正确的是（）

A、x•x²=x² B、（xy）²=xy² C、（x²）³=x⁶ D、x²+x²=x⁴

查看试题解析
5. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥1 B、x＞1 C、x＜1 D、x≤1

查看试题解析
6. 若三角形的两边长分别为6cm，9cm，则其第三边的长可能为（）

A、2cm B、3cm C、7cm D、16cm

查看试题解析
7. 以下各图均有彼此连接的六个小正方形纸片组成，其中不能折叠成一个正方体的是（）

A、 B、 C、 D、

查看试题解析
8. 下列事件中属于随机事件的是（）

A、抛出的篮球会落下 B、从装有黑球，白球的袋里摸出红球 C、367人中有2人是同月同日出生 D、买1张彩票，中500万大奖

查看试题解析
9. 如图，将边长为 $\sqrt{2}$ 的正方形ABCD沿对角线AC平移，使点A移至线段AC的中点A′处，得新正方形A′B′C′D′，新正方形与原正方形重叠部分（图中阴影部分）的面积是（）

A、 $\sqrt{2}$ B、 $\frac{1}{2}$ C、1 D、 $\frac{1}{4}$

查看试题解析
10. 平面直角坐标中，已知点O（0，0），A（0，2），B（1，0），点P是反比例函数y=﹣ $\frac{1}{x}$ 图象上的一个动点，过点P作PQ⊥x轴，垂足为Q．若以点O、P、Q为顶点的三角形与△OAB相似，则相应的点P共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 3⁰﹣2^﹣¹= ．

查看试题解析
12. 如图AB∥CD，AB与DE交于点F，∠B=40°，∠D=70°，则∠E= ．

查看试题解析
13. 若直角三角形的一个锐角为20°，则另一个锐角等于．

查看试题解析
14. 方程组 ${\begin{matrix} 3 x + y = 3 \\ 2 x - y = 2 \end{matrix}$ 的解为．

查看试题解析
15. 若方程x²+kx+9=0有两个相等的实数根，则k= ．

查看试题解析
16. 某班40名同学的年龄情况如下表，则这40名同学的年龄的中位数是岁．
年齡/岁
14
15
16
17
人数
4
16
18
2

查看试题解析
17.
如图，每个图案都由若干个棋子摆成，依照此规律，第n个图案中棋子的总个数可以用含n的代数式表示为．

查看试题解析
18. 已知⊙O的半径是5，圆心O到直线AB的距离为2，则⊙O上有且只有个点到直线AB的距离为3．

查看试题解析

三、解答题

19.

(1)、计算：（a﹣ $\frac{1}{a}$ ）÷ $\frac{a - 1}{a}$ ；

(2)、解不等式组： ${\begin{cases} x - 1 \geq 0 \\ 2 (x + 2) > 3 x \end{cases}$ ．

查看试题解析
20. 根据第5次、第6次人口普查的结果，2000年，2010年我国每10万人受教育程度的情况如下：
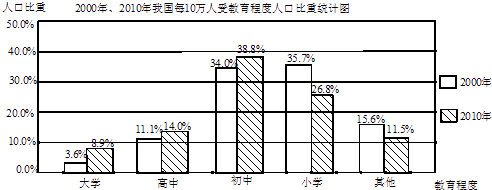
根据图中的信息，完成下列填空：

(1)、2010年我国具有高中文化程度的人口比重为；

(2)、2010年我国具有文化程度的人口最多；

(3)、同2000年相比，2010年我国具有文化程度的人口增幅最大．

查看试题解析
21. 小明骑自行车从家去学校，途经装有红、绿灯的三个路口．假设他在每个路口遇到红灯和绿灯的概率均为 $\frac{1}{2}$ ，则小明经过这三个路口时，恰有一次遇到红灯的概率是多少？请用树状图的方法加以说明．

查看试题解析
22. 徐州至上海的铁路里程为650km．从徐州乘“C”字头列车A，“D”字头列车B都可到达上海，已知A车的平均速度为B车的2倍，且行驶时间比B车少2.5h．

(1)、设A车的平均速度是xkm/h，根据题意，可列分式方程：；

(2)、求A车的平均速度及行驶时间．

查看试题解析
23. 如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．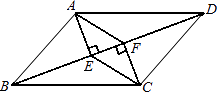

(1)、求证：△ABE≌△CDF；

(2)、若AC与BD交于点O，求证：AO=CO．

查看试题解析
24. 如图，PA，PB是⊙O的两条切线，切点分别为A，B，OP交AB于点C，OP=13，sin∠APC= $\frac{5}{13}$ ．

(1)、求⊙O的半径；

(2)、求弦AB的长．

查看试题解析
25. 某网店以每件60元的价格购进一批商品，若以单价80元销售，每月可售出300件，调查表明：单价每上涨1元，该商品每月的销量就减少10件．

(1)、请写出每月销售该商品的利润y（元）与单价上涨x（元）件的函数关系式；

(2)、单价定为多少元时，每月销售该商品的利润最大？最大利润为多少？

查看试题解析
26. 如图，将矩形纸片ABCD按如下的顺序进行折叠：对折，展平，得折痕EF（如图①）；沿CG折叠，使点B落在EF上的点B′处，（如图②）；展平，得折痕GC（如图③）；沿GH折叠，使点C落在DH上的点C′处，（如图④）；沿GC′折叠（如图⑤）；展平，得折痕GC′，GH（如图 ⑥）．

(1)、求图 ②中∠BCB′的大小；

(2)、图⑥中的△GCC′是正三角形吗？请说明理由．

查看试题解析
27. 如图①，在△ABC中，AB=AC，BC=acm，∠B=30°．动点P以1cm/s的速度从点B出发，沿折线B﹣A﹣C运动到点C时停止运动．设点P出发x s时，△PBC的面积为y cm² ．已知y与x的函数图象如图②所示．请根据图中信息，解答下列问题：

(1)、试判断△DOE的形状，并说明理由；

(2)、当a为何值时，△DOE与△ABC相似？

查看试题解析
28.
如图，已知二次函数y=x²+bx+c的图象与x轴交于A，B两点，与y轴交于点P，顶点为C（1，﹣2）．

(1)、求此函数的关系式；

(2)、作点C关于x轴的对称点D，顺次连接A，C，B，D．若在抛物线上存在点E，使直线PE将四边形ACBD分成面积相等的两个四边形，求点E的坐标；

(3)、在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由．

查看试题解析

年齡/岁	14	15	16	17
人数	4	16	18	2