2011年江苏省宿迁市中考数学试卷
试卷更新日期：2017-05-18 类型：中考真卷
一、选择题
-
1. 下列各数中，比0小的数是（ ）A、﹣1 B、1 C、 D、π2. 在平面直角坐标系中，点M（﹣2，3）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列所给的几何体中，主视图是三角形的是（ ）A、
B、
C、
D、
4. 计算（﹣a3）2的结果是（ ）A、﹣a5 B、a5 C、a6 D、﹣a65. 方程 的解是（ ）A、﹣1 B、2 C、1 D、06. 如图，将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域，若指针固定不变，转动这个转盘一次（如果指针指在等分线上，那么重新转动，直至指针指在某个扇形区域内为止），则指针指在甲区域内的概率是（ ）
A、1 B、 C、 D、7. 如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）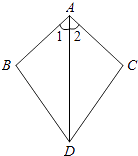
A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA8. 已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（ ）
A、a＞0 B、当x＞1时，y随x的增大而增大 C、c＜0 D、3是方程ax2+bx+c=0的一个根二、填空题
-
9. 实数 的倒数是10. 函数y= 中，自变量x的取值范围是11. 将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如图所示）．若∠C=90°，BC=8cm，则折痕DE的长度是 cm．
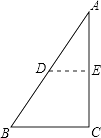12. 某校为鼓励学生课外阅读，制定了“阅读奖励方案”．方案公布后，随机征求了100名学生的意见，并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计，绘制成如图所示的扇形统计图．若该校有1000名学生，则赞成该方案的学生约有人．
13. 如图，把一个半径为12cm的圆形硬纸片等分成三个扇形，用其中一个扇形制作成一个圆锥形纸筒的侧面（衔接处无缝隙且不重叠），则圆锥底面半径是 cm．
14. 在平面直角坐标系中，已知点A（﹣4，0）、B（0，2），现将线段AB向右平移，使A与坐标原点O重合，则B平移后的坐标是 ．15. 如图，在梯形ABCD中，AB∥DC，∠ADC的平分线与∠BCD的平分线的交点E恰在AB上．若AD=7cm，BC=8cm，则AB的长度是 cm．
16. 如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m．若矩形的面积为4m2 ， 则AB的长度是 m（可利用的围墙长度超过6m）．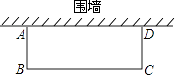
17. 如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC．若∠A=26°，则∠ACB的度数为 ．
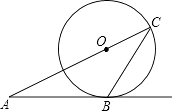18.一个边长为16m的正方形展厅，准备用边长分别为1m和0.5m的两种正方形地板砖铺设其地面．要求正中心一块是边长为1m的大地板砖，然后从内到外一圈小地板砖、一圈大地板砖相间镶嵌（如图所示），则铺好整个展厅地面共需要边长为1m的大地板砖块．
三、解答题
-
19. 计算：|﹣2|+（﹣2）0+2sin30°．20. 解不等式组 ．21. 已知实数a、b满足ab=1，a+b=2，求代数式a2b+ab2的值．22. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；(2)、分别计算甲、乙六次测试成绩的方差；(3)、根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．（计算方差的公式：s2= [ ]）
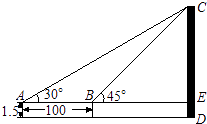
23.如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取 =1.732，结果精确到1m）
24. 在一个不透明的布袋中装有相同的三个小球，其上面分别标注数字1、2、3、，现从中任意摸出一个小球，将其上面的数字作为点M的横坐标；将球放回袋中搅匀，再从中任意摸出一个小球，将其上面的数字作为点M的纵坐标．(1)、写出点M坐标的所有可能的结果；(2)、求点M在直线y=x上的概率；(3)、求点M的横坐标与纵坐标之和是偶数的概率．25. 某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．
(1)、有月租费的收费方式是（填①或②），月租费是元；(2)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式；(3)、请你根据用户通讯时间的多少，给出经济实惠的选择建议．
26. 如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y= （x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、B．
(1)、判断P是否在线段AB上，并说明理由；(2)、求△AOB的面积；(3)、Q是反比例函数y= （x＞0）图象上异于点P的另一点，请以Q为圆心，QO半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．27. 如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ=t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．
(1)、当t≠1时，求证：△PEQ≌△NFM；(2)、顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．28. 如图，在Rt△ABC中，∠B=90°，AB=1，BC= ，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．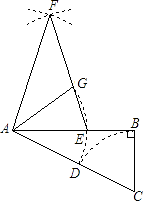
(1)、求AE的长度；(2)、分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，试猜想∠EAG的大小，并说明理由．