2011年江苏省泰州市中考数学试卷
试卷更新日期:2017-05-18 类型:中考真卷
一、选择题
-
1. 的相反数是( )A、 B、﹣2 C、 D、22. 计算2a2•a3的结果是( )A、2a5 B、2a6 C、4a5 D、4a63. 一元二次方程x2=2x的根是( )A、x=2 B、x=0 C、x1=0,x2=2 D、x1=0,x2=﹣24. 如图是一个几何体的三视图,则这个几何体是( )
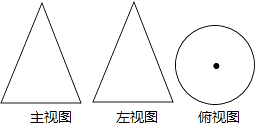 A、圆锥 B、圆柱 C、长方体 D、球体5. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 ,这个函数的图象大致是( )A、
A、圆锥 B、圆柱 C、长方体 D、球体5. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 ,这个函数的图象大致是( )A、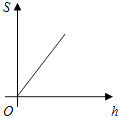 B、
B、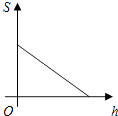 C、
C、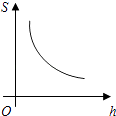 D、
D、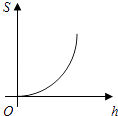 6. 为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是( )A、某市八年级学生的肺活量 B、从中抽取的500名学生的肺活量 C、从中抽取的500名学生 D、5007. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:
6. 为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是( )A、某市八年级学生的肺活量 B、从中抽取的500名学生的肺活量 C、从中抽取的500名学生 D、5007. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;
②AB=CD,AD=BC;
③AO=CO,BO=DO;
④AB∥CD,AD=BC.
其中一定能判断这个四边形是平行四边形的条件共有( )
A、1组 B、2组 C、3组 D、4组8. 如图,直角三角形纸片ABC的∠C为90°,将三角形纸片沿着图示的中位线DE剪开,然后把剪开的两部分重新拼接成不重叠的图形,下列选项中不能拼出的图形是( )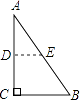 A、平行四边形 B、矩形 C、等腰梯形 D、直角梯形
A、平行四边形 B、矩形 C、等腰梯形 D、直角梯形二、填空题
-
9. 分解因式:2a2﹣4a= .10. 不等式2x+1>﹣5的解集是11. 一个多项式与m2+m﹣2的和是m2﹣2m.这个多项式是 .12. 点P(﹣3,2)关于x轴对称的点P′的坐标是 .13. 甲、乙两位同学参加跳远训练,在相同条件下各跳了6次,统计平均数 ,方差S甲2<S乙2 , 则成绩较稳定的同学是(填“甲”或“乙”).14. 如图,直线a、b被直线l所截,a∥b,∠1=70°,则∠2= .
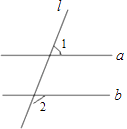 15. 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是平方单位(结果保留π).
15. 如图,△ABC的3个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则线段AB扫过的图形面积是平方单位(结果保留π).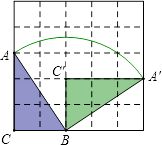 16.
16.“一根弹簧原长10cm,在弹性限度内最多可挂质量为5kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比,
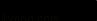 ,则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染,被污染的部分是确定函数关系式的一个条件,你认为该条件可以是:(只需写出1个).17. 如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1、l4上,该正方形的面积是平方单位.
,则弹簧的总长度y(cm)与所挂物体质量x(kg)之间的函数关系式为y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时发现部分内容被墨迹污染,被污染的部分是确定函数关系式的一个条件,你认为该条件可以是:(只需写出1个).17. 如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1、l4上,该正方形的面积是平方单位.
三、解答题
-
18. 计算或化简:(1)、 ,(2)、 .19. 解方程组 ,并求 的值.20. 一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出1个球,记录下颜色后放回袋中并搅匀,再从中任意摸出1个球.请用画树状图的方法列出所有可能的结果,并写出两次摸出的球颜色相同的概率.21. 某文具商店共有单价分别为10元、15元和20元的3种文具盒出售,该商店统计了2011年3月份这3种文具盒的销售情况,并绘制统计图如下:
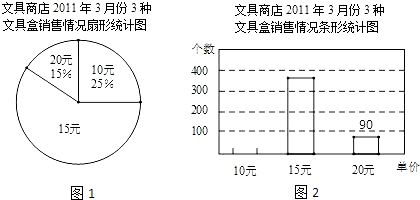 (1)、请在图②中把条形统计图补充完整.(2)、小亮认为:该商店3月份这3种文具盒总的平均销售价格为 (元),你认为小亮的计算方法正确吗?如不正确,请计算出总的平均销售价格.22. 一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.
(1)、请在图②中把条形统计图补充完整.(2)、小亮认为:该商店3月份这3种文具盒总的平均销售价格为 (元),你认为小亮的计算方法正确吗?如不正确,请计算出总的平均销售价格.22. 一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.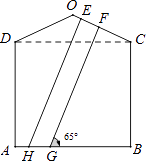 (1)、求证:GF⊥OC;(2)、求EF的长(结果精确到0.1m).
(1)、求证:GF⊥OC;(2)、求EF的长(结果精确到0.1m).(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
23. 如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.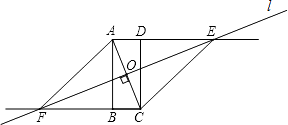 (1)、△ABC与△FOA相似吗?为什么?(2)、试判定四边形AFCE的形状,并说明理由.24. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)、△ABC与△FOA相似吗?为什么?(2)、试判定四边形AFCE的形状,并说明理由.24. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.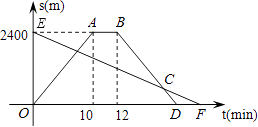 (1)、求s2与t之间的函数关系式;(2)、小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?25. 如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.
(1)、求s2与t之间的函数关系式;(2)、小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?25. 如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N. (1)、点N是线段BC的中点吗?为什么?(2)、若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.26. 已知二次函数y=x2+bx﹣3的图象经过点P(﹣2,5)(1)、求b的值并写出当1<x≤3时y的取值范围;(2)、设P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图象上,
(1)、点N是线段BC的中点吗?为什么?(2)、若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.26. 已知二次函数y=x2+bx﹣3的图象经过点P(﹣2,5)(1)、求b的值并写出当1<x≤3时y的取值范围;(2)、设P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图象上,①当m=4时,y1、y2、y3能否作为同一个三角形三边的长?请说明理由;
②当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,请说明理由.
27. 在平面直角坐标系xOy中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.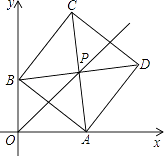 (1)、当∠BAO=45°时,求点P的坐标;(2)、求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;(3)、设点P到x轴的距离为h,试确定h的取值范围,并说明理由.
(1)、当∠BAO=45°时,求点P的坐标;(2)、求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;(3)、设点P到x轴的距离为h,试确定h的取值范围,并说明理由.