2011年江苏省苏州市中考数学试卷
试卷更新日期:2017-05-18 类型:中考真卷
一、选择题
-
1. 2×(﹣ )的结果是( )A、﹣4 B、﹣1 C、 D、2. △ABC的内角和为( )A、180° B、360° C、540° D、720°3. 地球上的海洋面积约为361000000千米2 , 将361000000这个数用科学记数法表示为( )A、3.61×108 B、3.61×107 C、361×107 D、0.361×1094. 若m•23=26 , 则m等于( )A、2 B、4 C、6 D、85. 有一组数椐:3,4,5,6,6,则下列四个结论中正确的是( )A、这组数据的平均数、众数、中位数分别是4.8,6,6 B、这组数据的平均数、众数、中位数分别是5,5,5 C、这组数据的平均数、众数、中位数分别是4.8,6,5 D、这组数据的平均数、众数、中位数分别是5,6,66. 不等式组 的所有整数解之和是( )A、9 B、12 C、13 D、157. 已知 ,则 的值是( )A、 B、﹣ C、2 D、﹣28. 下列四个结论中,正确的是( )A、方程x+ =﹣2有两个不相等的实数根 B、方程x+ =1有两个不相等的实数根 C、方程x+ =2有两个不相等的实数根 D、方程x+ =a(其中a为常数,且|a|>2)有两个不相等的实数根9. 如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
 A、 B、 C、 D、10. 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A、 B、 C、 D、10. 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )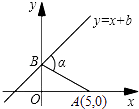 A、3 B、 C、4 D、
A、3 B、 C、4 D、二、填空题
-
11. 因式分解:a2﹣9= .
12. 如图,在四边形ABCD中,AB∥CD,AD∥BC,AC、BD相交于点0.若AC=6,则线段AO的长度等于 .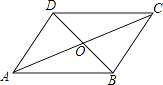 13. 某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有人.
13. 某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有人.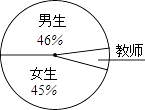 14. 函数y= 的自变量x的取值范围是 .15. 已知a、b是一元二次方程x2﹣2x﹣1=0的两个实数根,则代数式(a﹣b)(a+b﹣2)+ab的值等于 .16. 如图,已知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD= ,则线段BC的长度等于 .
14. 函数y= 的自变量x的取值范围是 .15. 已知a、b是一元二次方程x2﹣2x﹣1=0的两个实数根,则代数式(a﹣b)(a+b﹣2)+ab的值等于 .16. 如图,已知AB是⊙O的一条直径,延长AB至C点,使得AC=3BC,CD与⊙O相切,切点为D.若CD= ,则线段BC的长度等于 .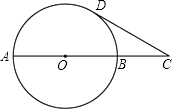 17. 如图,已知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
17. 如图,已知△ABC是面积为 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).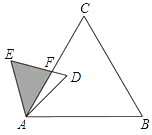 18. 如图,已知点A的坐标为( ,3),AB丄x轴,垂足为B,连接OA,反比例函数y= (k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的 倍的长为半径作圆,则该圆与x轴的位置关系是(填”相离”,“相切”或“相交“).
18. 如图,已知点A的坐标为( ,3),AB丄x轴,垂足为B,连接OA,反比例函数y= (k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的 倍的长为半径作圆,则该圆与x轴的位置关系是(填”相离”,“相切”或“相交“).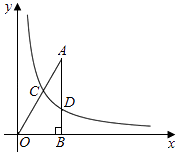
三、解答题
-
19. 计算:22+|﹣1|﹣ .20. 解不等式:3﹣2(x﹣1)<1.21. 先化简,再求值:(a﹣1+ )÷(a2+1),其中a= ﹣1.22. 已知|a﹣1|+ =0,求方裎 +bx=1的解.23. 如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
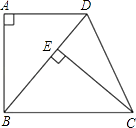 (1)、求证:△ABD≌△ECB;(2)、若∠DBC=50°,求∠DCE的度数.24. 如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同
(1)、求证:△ABD≌△ECB;(2)、若∠DBC=50°,求∠DCE的度数.24. 如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同 (1)、一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;(2)、现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?25. 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)、一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;(2)、现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?25. 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.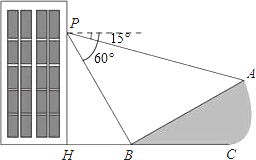 (1)、山坡坡角(即∠ABC)的度数等于度;(2)、求A、B两点间的距离(结果精确到0.1米,参考数据: ≈1.732).26. 如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)、山坡坡角(即∠ABC)的度数等于度;(2)、求A、B两点间的距离(结果精确到0.1米,参考数据: ≈1.732).26. 如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD. (1)、弦长AB等于(结果保留根号);(2)、当∠D=20°时,求∠BOD的度数;(3)、当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.27. 已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
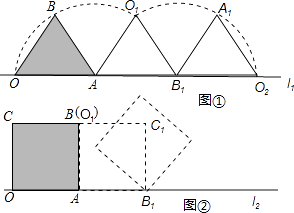
(1)、弦长AB等于(结果保留根号);(2)、当∠D=20°时,求∠BOD的度数;(3)、当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.27. 已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.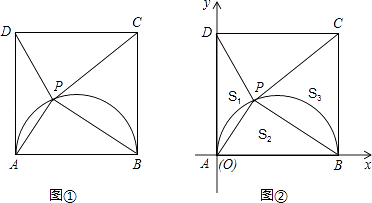 (1)、如图①,当PA的长度等于时,∠PAD=60°;当PA的长度等于时,△PAD是等腰三角形;(2)、如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3 . 设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.28. 如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线l1上.OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺吋针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1 , 绕点B1按顺吋针方向旋转 120°,此时点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
(1)、如图①,当PA的长度等于时,∠PAD=60°;当PA的长度等于时,△PAD是等腰三角形;(2)、如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3 . 设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.28. 如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线l1上.OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺吋针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1 , 绕点B1按顺吋针方向旋转 120°,此时点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).小慧还发现:三角形纸片在上述两次旋转的过程中.顶点O运动所形成的图形是两段圆弧,即 和 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片0ABC放在直线l2上,0A边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B2处,小慧又将正方形纸片 AO1C1B1绕顶点B1按顺时针方向旋转90°,….按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片0ABC按上述方法经过3次旋转,求顶点0经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形纸片OABC按上述方法经过5次旋转.求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点0经过的路程是 ?
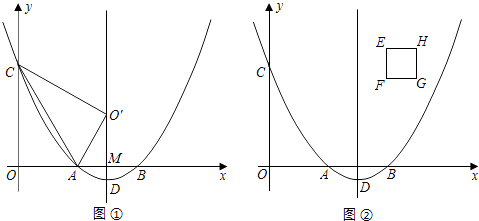
 29. 已知二次函数y=a(x2﹣6x+8)(a>0)的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.(1)、如图①.连接AC,将△OAC沿直线AC翻折,若点O的对应点0'恰好落在该抛物线的 对称轴上,求实数a的值;(2)、如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的 右侧.小林同学经过探索后发现了一个正确的命题:“若点P是边EH或边HG上的任意一点,则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等 (即这四条线段不能构成平行四边形).“若点P是边EF或边FG上的任意一点,刚才的结论是否也成立?请你积极探索,并写出探索过程;(3)、如图②,当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是否存在一个正数a,使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等 (即这四条线段能构成平行四边形)?请说明理由.
29. 已知二次函数y=a(x2﹣6x+8)(a>0)的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.(1)、如图①.连接AC,将△OAC沿直线AC翻折,若点O的对应点0'恰好落在该抛物线的 对称轴上,求实数a的值;(2)、如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的 右侧.小林同学经过探索后发现了一个正确的命题:“若点P是边EH或边HG上的任意一点,则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等 (即这四条线段不能构成平行四边形).“若点P是边EF或边FG上的任意一点,刚才的结论是否也成立?请你积极探索,并写出探索过程;(3)、如图②,当点P在抛物线对称轴上时,设点P的纵坐标t是大于3的常数,试问:是否存在一个正数a,使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等 (即这四条线段能构成平行四边形)?请说明理由.