2011年江苏省南京市中考数学试卷
试卷更新日期:2017-05-18 类型:中考真卷
一、选择题
-
1. 的值等于( )A、3 B、﹣3 C、±3 D、2. 下列运算正确的是( )
A、a2+a3=a5 B、a2•a3=a6 C、a3+a2=a D、(a2)3=a63. 在第六次全国人口普查中,南京市常住人口约为800万人,其中65岁及以上人口占9.2%,则该市65岁及以上人口用科学记数法表示约为( )A、0.736×106人 B、7.36×104人 C、7.36×105人 D、7.36×106人4. 为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )A、随机抽取该校一个班级的学生 B、随机抽取该校一个年级的学生 C、随机抽取该校一部分男生 D、分别从该校初一、初二、初三年级中各随机抽取10%的学生5.如图是一个三棱柱.下列图形中,能通过折叠围成一个三棱柱的是( )
 A、
A、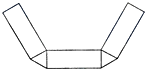 B、
B、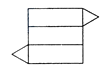 C、
C、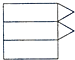 D、
D、 6.
6.如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
 A、2 B、2+ C、2 D、2+
A、2 B、2+ C、2 D、2+二、填空题
-
7. ﹣2的相反数是8. 如图,过正五边形ABCDE的顶点A作直线l∥CD,则∠1= .
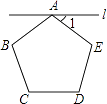 9. 计算( +1)(2﹣ )= .10. 等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为 cm.11. 如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于 .
9. 计算( +1)(2﹣ )= .10. 等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为 cm.11. 如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于 .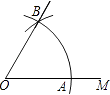 12. 如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为 cm2 .
12. 如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为 cm2 .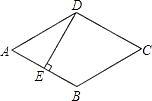 13. 如图,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.为了避免触礁,轮船P与A、B的张角∠APB的最大值为 .
13. 如图,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.为了避免触礁,轮船P与A、B的张角∠APB的最大值为 .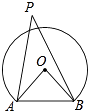 14. 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α( 0°<α<180°),则∠α= .
14. 如图,E、F分别是正方形ABCD的边BC、CD上的点,BE=CF,连接AE、BF.将△ABE绕正方形的中心按逆时针方向旋转到△BCF,旋转角为α( 0°<α<180°),则∠α= .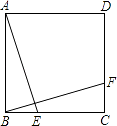 15. 设函数y= 与y=x﹣1的图象的交点坐标为(a,b),则 ﹣ 的值为16. 甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:
15. 设函数y= 与y=x﹣1的图象的交点坐标为(a,b),则 ﹣ 的值为16. 甲、乙、丙、丁四位同学围成一圈依序循环报数,规定:①甲、乙、丙、丁首次报出的数依次为1、2、3、4,接着甲报5,乙报6…按此规律,后一位同学报出的数比前一位同学报出的数大1.当报到的数是50时,报数结束;
②若报出的数为3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需拍手的次数为 .
三、解答题
-
17. 解不等式组 ,并写出不等式组的整数解.18. 计算( ﹣ )÷ .19. 解方程:x2﹣4x+1=0.20. 某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下.
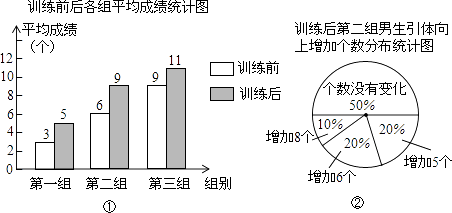 (1)、求训练后第一组平均成绩比训练前增长的百分数;(2)、小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;(3)、你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.21. 如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)、求训练后第一组平均成绩比训练前增长的百分数;(2)、小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;(3)、你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.21. 如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.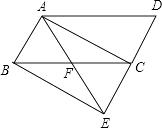 (1)、求证:△ABF≌△ECF;(2)、若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.22. 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系.
(1)、求证:△ABF≌△ECF;(2)、若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.22. 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系. (1)、小亮行走的总路程是 m,他途中休息了 min;(2)、①当50≤x≤80时,求y与x的函数关系式;
(1)、小亮行走的总路程是 m,他途中休息了 min;(2)、①当50≤x≤80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
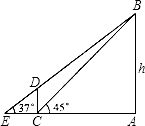
23. 从3名男生和2名女生中随机抽取2014年南京青奥会志愿者.求下列事件的概率:(1)、抽取1名,恰好是女生;(2)、抽取2名,恰好是1名男生和1名女生.24. 已知函数y=mx2﹣6x+1(m是常数).(1)、求证:不论m为何值,该函数的图象都经过y轴上的一个定点;(2)、若该函数的图象与x轴只有一个交点,求m的值.25.如图,某数学课外活动小组测量电视塔AB的高度.他们借助一个高度为30m的建筑物CD进行测量,在点C处测得塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 26. 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
26. 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.P为BC的中点,动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.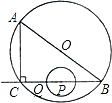 (1)、当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)、已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.27. 如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
(1)、当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;(2)、已知⊙O为△ABC的外接圆.若⊙P与⊙O相切,求t的值.27. 如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.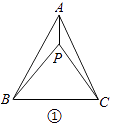 (1)、如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;
(1)、如图②,已知Rt△ABC中,∠ACB=90°,∠ABC>∠A,CD是AB上的中线,过点B作BE丄CD,垂足为E.试说明E是△ABC的自相似点;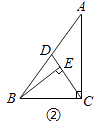 (2)、在△ABC中,∠A<∠B<∠C.
(2)、在△ABC中,∠A<∠B<∠C.①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.
 28. 【问题情境】
28. 【问题情境】已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ )(x>0).
【探索研究】
(1)、我们可以借鉴以前研究函数的经验,先探索函数y=x+ (x>0)的图象和性质.①填写下表,画出函数的图象;
x
…
1
2
3
4
…
y
…
…
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数y=x+ (x>0)的最小值.
(2)、用上述方法解决“问题情境”中的问题,直接写出答案.