广东省深圳市坪山新区2017届九年级下学期第二次调研数学试卷

试卷更新日期：2017-05-18 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的负倒数（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 2016年10月28日，随着深圳地铁7，9号线的相继开通，深圳地铁日均客流量达到470万人次，则470万用科学记数法表示为（）

A、47×10⁴ B、47×10⁵ C、4.7×10⁵ D、4.7×10⁶

查看试题解析
3. 下列图形中，是中心对称但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 不等式组 ${\begin{matrix} 2 x+ 1 \leq 3 \\ x > - 3 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（）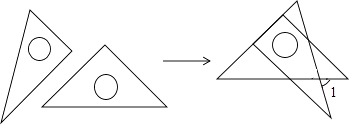

A、75° B、60° C、45° D、30°

查看试题解析
6. 一个多边形的内角和是720°，这个多边形的边数是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 一元二次方程 $2 x^{2} - 3 x + 1 = 0$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 某服装厂准备加工400套运动装，加工完160套后，采用新技术工作效率比原计划提高提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套，则根据题意可得方程为（）

A、 $\frac{160}{x} + \frac{400 - 160}{(1 + 20 %) x} = 18$ B、 $\frac{160}{x} + \frac{400}{(1 + 20 %)} = 18$ C、 $\frac{160}{x} + \frac{400 - 160}{20 % x} = 18$ D、 $\frac{400}{x} + \frac{400 - 160}{(1 + 20 %) x} = 18$

查看试题解析
9.
如图，A，B，C，D为⊙O的四等分点，动点P从圆心O出发，沿O﹣C﹣D﹣O路线作匀速运动，设运动时间为t（秒）．∠APB=y（度），则下列图象中表示y与t之间函数关系最恰当的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，平行四边形ABCD中，E是AD上的一点，且AE= $\frac{1}{3}$ AD，对角线AC，BD交于点O，EC交BD于F，BE交AC于G，如果平行四边形ABCD的面积为S，那么，△GEF的面积为（）

A、 $\frac{1}{10} S$ B、 $\frac{1}{15} S$ C、 $\frac{1}{20} S$ D、 $\frac{1}{30} S$

查看试题解析
11. 定义：若点P(a，b)在函数y＝ $\frac{1}{x}$ 的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y＝ax²＋bx称为函数y＝的一个“派生函数”．例如：点(2， $\frac{1}{2}$ )在函数y＝ $\frac{1}{x}$ 的图象上，则函数y＝2x²＋x称为函数y＝ $\frac{1}{x}$ 的一个“派生函数”．现给出以下两个命题：(1)存在函数y＝ $\frac{1}{x}$ 的一个“派生函数”，其图象的对称轴在y轴的右侧；(2)函数y＝ $\frac{1}{x}$ 的所有“派生函数”的图象都经过同一点．下列判断正确的是（）

A、命题（1）与命题（2）都是真命题 B、命题（1）与命题（2）都是假命题 C、命题（1）是假命题，命题（2）是真命题 D、命题(1)是真命题，命题(2)是假命题

查看试题解析
12. 已知抛物线 $y = k (x + 1) (x - \frac{3}{k})$ 与 $x$ 轴交于点A、B，与 $y$ 轴交于点C，则能使△ABC为等腰三角形抛物线的条数是（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题：

13. 因式分解： $2 a^{2} - 18 =$ ．

查看试题解析
14.
如图，在扇形AOB中，∠AOB=90⁰ ，以点A为圆心， OA的长为半径作 $\overset{⌢}{O C}$ 交 $\overset{⌢}{A B}$ 于点C，若OA=2，则阴影部分的面积是．

查看试题解析
15. 我们把分子为1的分数叫做理想分数，如 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{4}$ ，…，任何一个理想分数都可以写成两个不同理想分数的和，如 $\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$ ， $\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$ ， $\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$ ，…根据对上述式子的观察，请你思考：如果理想分数 $\frac{1}{n} = \frac{1}{a} + \frac{1}{b}$ (n是不小于2的整数，且a＜b)，那么b－a＝． (用含n的式子表示)

查看试题解析
16. 将函数 $y = 2 x + b$ （b为常数）的图象位于 $x$ 轴下方的部分沿 $x$ 轴翻折至其上方后，所得的折线是函数 $y = | 2 x + b |$ （b为常数）的图象．若该图象在直线y＝2下方的点的横坐标 $x$ 满足 $0 < x < 3$ ，则b的取值范围为．

查看试题解析

三、三、解答题

17. 综合题

(1)、计算 ${(- \frac{1}{3})}^{- 2} - 2 \cos 45^{0} + {(\frac{π - 3.14}{2})}^{0} + \frac{1}{2} \sqrt{8} + {(- 1)}^{2017}$

(2)、先化简，再求值 $\frac{a}{a - 1} - \frac{3 a - 1}{a^{2} - 1}$ ,其中 $a = \sqrt{2} - 1$

查看试题解析
18. 某校初三（1）班 $50$ 名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：
自选项目
人数
频率
立定跳远
9
0.18
三级蛙跳
12
$a$
一分钟跳绳
8
0.16
投掷实心球
$b$
0.32
推铅球
5
0.1
合计
50
1

(1)、求 $a ， b$ 的值；

(2)、若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；

(3)、在选报“推铅球”的学生中，有3名男生，2名女生.为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多有一名女生的概率.

查看试题解析
19.
如图所示，在 $R t Δ ACB 中， ∠ C = 90^{°} ， AC = 3 ， BC = 2 ， AD 为中线 .$

(1)、比较∠BAD和∠DAC的大小。

(2)、求sin∠BAD

查看试题解析
20. “低碳生活，绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.

(1)、若1月份到4月份新投放单车数量的月平均增长率相同，3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆？

(2)、考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A，B两种规格的自行车100辆，已知A型的进价为500元/辆，售价为700元/辆，B型车进价为1000元/辆，售价为1300元/辆。假设所进车辆全部售完，为了使利润最大，该商城应如何进货？

查看试题解析
21.
如图，已知一次函数y= $\frac{3}{2}$ x﹣3与反比例函数 $y = \frac{k}{x}$ 的图象相交于点A（4，n），与 $x$ 轴相交于点B．

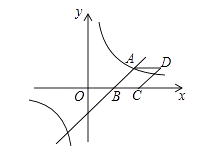(1)、填空：n的值为， k的值为；

(2)、以AB为边作菱形ABCD，使点C在 $x$ 轴正半轴上，点D在第一象限，求点D的坐标；

(3)、考察反比函数 $y = \frac{k}{x}$ 的图象，当 $y \geq - 2$ 时，请直接写出自变量 $x$ 的取值范围．

查看试题解析
22.
如图所示， $Rt Δ ABC$ 中，∠BAC=90°，∠C=30°，BC=2，⊙O是△ABC的外接圆，D是CB延长线上一点，且BD=1，连接DA，点P是射线DA上的动点。

(1)、求证DA是⊙O的切线；

(2)、DP的长度为多少时，∠BPC的度数最大，最大度数是多少？请说明理由。

(3)、点P运动的过程中，（PB+PC）的值能否达到最小，若能，求出这个最小值，若不能，说明理由.

查看试题解析
23.
如图，顶点为（1，4）的抛物线y=ax²+bx+c与直线y= $\frac{1}{2}$ x+n交于点A（2，2），直线y= $\frac{1}{2}$ x+n与y轴交于点B与x轴交于点C

(1)、求n的值及抛物线的解析式

(2)、P为抛物线上的点，点P关于直线AB的对称轴点在x轴上，求点P的坐标

(3)、点D为x轴上方抛物线上的一点，点E为轴上一点，以A、B、E、D为顶点的四边为平行四边形时，直接写出点E的坐标．

查看试题解析

自选项目	人数	频率
立定跳远	9	0.18
三级蛙跳	12	$a$
一分钟跳绳	8	0.16
投掷实心球	$b$	0.32
推铅球	5	0.1
合计	50	1