浙江省台州市2018-2019学年八年级上学期教学质量检测（二）
试卷更新日期：2019-05-10 类型：期末考试
一、单选题
-
1. 下列有关整式运算正确的是（ ）
A、 ( x3 )2 = x5 B、 (2x)2 = 2x2 C、 ( x + 1) 2 = x2 + 1 D、x3 × x2 = x52. 下列由左到右的变形，属于因式分解的是（ ）A、( x + 2)( x - 2) = x2 - 4 B、x2 - 4 = ( x + 2)( x - 2) C、x2 - 4 + 3x = ( x + 2)( x - 2) + 3x D、x2 + 4x - 2 = x ( x + 4) - 23. 用科学记数法表示 0.000 006 1，结果是（ ）A、6.1×10－5 B、6.1×10－6 C、0.61×10－5 D、61×10－74. 下列四个多项式中，能进行因式分解的是（ ）A、 a2 + 4 B、 a2 - 4a + 4 C、 x2 + 5 y D、 x2 - 5 y5. 若代数式 2a2 + 3a + 1 的值为 2，则代数式 4a2 + 6a + 5 的值为（ ）
A、4 B、5 C、6 D、76. 把多项式(m+1)(m－1)+(m－1)提取公因式(m－1)后，余下的部分是（ ）A、m+1 B、2m C、2 D、m+27. 下列多项式：①16x2 - x ；② ( x -1)2 - 4( x -1) ；③ ( x + 1)2 - 4x ( x + 1) + 4x2 ；④ -4x2 -1 + 4x ，因式分解后，结果中含有相同因式的是（ ）
A、 ①和② B、③和④ C、①和④ D、②和③8. 如图，边长为a，b的矩形的周长为14，面积为10，则a2b+ab2的值为（ ）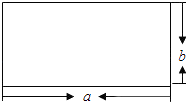
A、140 B、70 C、35 D、249. 若 a+b=4，ab=3，则 a2+b2 的值为（ ）
A、10 B、13 C、16 D、2210. 已知 ( x + 3)2 + ( x - 7)2 = 58 ，则 ( x + 3)( x - 7) 的值是（ ）
A、21 B、28 C、－21 D、－28二、填空题
-
11. 计算： x6 ÷x4 = ．
12. 分解因式： x2 - 4x + 4 = ； 4x2 - 36 = ．13. 已知二次三项式 x2 + mx + 9 能用完全平方公式分解因式，则 m= ．
14. 化简：(b－1)(b+1)(b2+1)= ．15. 若一个正整数能表示为两个正整数的平方差，则称这个正整数为“智慧数”（如3 = 22 -12 ，16 = 52 - 32 ）．如下为部分按一定规律排列的“智慧数”：3，5，7，8，9，11，…．则第 9 个“智慧数”是 ．
16. 关于 x 的代数式 (3 - ax)( x2 + 2x -1) 的展开式中不含 x2 项，则 a= ．
17. 计算： = ．18. 已知 2a = 4 ， 2b = 8 ，2x=16，若用含 a、b 的代数式表示 x，则 x= ．三、解答题
-
19. 计算 ：(1)、(2)、(3)、20.
(1)、计算： x × x3 - ( x2 )2 ；
(2)、因式分解： ax2 + 2axy + ay2 ．
21. 先化简，再求值： ( x + y )2 - x × ( x - y ) - y2 ，其中 x=1，y=－2．
22. 已知 x = + 3 ， y = - 3 ，求下列各式的值：(1)、x2 - 2xy + y2
(2)、x2 - y2
23. 仔细阅读下面例题，解答问题：例题：已知二次三项式 x2 - 4x + m 有一个因式是(x+3)，求另一个因式以及 m 的值．
解：设另一个因式为(x+n)，得 x2 - 4x + m = ( x + 3)( x + n)
则 x2 - 4x + m = x2 + (n + 3) x + 3n
∴
解得：n=－7，m=－21
∴另一个因式为(x－7)，m 的值为－21．
问题：仿照以上方法解答下面问题：
已知二次三项式 2x2 + 3x - k 有一个因式是(2x－3)，求另一个因式以及 k 的值．
24. 如图，长为 m ， 宽为 x(m>x)的大长方形被分割成 7 小块，除阴影 A，B 外，其 余 5 块是形状、大小完全相同的小长方形，其较短一边长为 y ． 记阴影 A 与 B 的面积差 为 S ．
(1)、分别用含 m ， x ， y 的代数式表示阴影 A，B 的面积；(2)、先化简 S ， 再求当 m=6，y=1 时 S 的值；(3)、当 x 取任何实数时，面积差 S 的值都保持不变，问 m 与 y 应满足什么条件？