2019年广东省广州市中考数学模拟预测卷3
试卷更新日期:2019-05-09 类型:中考模拟
一、选择题
-
1. 已知:|x|=3,|y|=2,且x>y,则x﹣y的值为( )A、5 B、1 C、5或1 D、﹣5或﹣12.
中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )
 A、
A、 B、
B、 C、
C、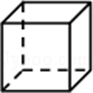 D、
D、 3. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1054. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
3. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1054. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、
B、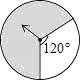 C、
C、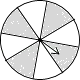 D、
D、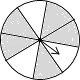 5. 有理式① ,② ,③
5. 有理式① ,② ,③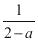 ,④ 中,是分式的有() A、①② B、③④ C、①③ D、①②③④6. 若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为( )A、6 B、-6 C、12 D、-127. 如图,正方形ABCD的面积是( )
,④ 中,是分式的有() A、①② B、③④ C、①③ D、①②③④6. 若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为( )A、6 B、-6 C、12 D、-127. 如图,正方形ABCD的面积是( )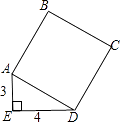 A、5 B、25 C、7 D、108. 一次函数y=2x+1的图象不经过第( )象限A、一 B、二 C、三 D、四9. 已知:二次函数 ,下列说法错误的是( )
A、5 B、25 C、7 D、108. 一次函数y=2x+1的图象不经过第( )象限A、一 B、二 C、三 D、四9. 已知:二次函数 ,下列说法错误的是( )
A、当 时,y随x的增大而减小 B、若图象与x轴有交点,则 C、当 时,不等式 的解集是 D、若将图象向上平移1个单位,再向左平移3个单位后过点 ,则10. 我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:指数运算
21=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
根据上表规律,某同学写出了三个式子:( )
①log216=4,②log525=5,③log2 =﹣1.其中正确的是
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 已知a2+a﹣3=0,那么a2(a+4)的值是12. 若x,y为实数,且满足(x+2y)2+ =0,则xy的值是 .13. 已知直线 ,将一块含 角的直角三角板 按如图方式放置( ),其中 , 两点分别落在直线 , 上,若∠2=52°,则∠1的度数为 .
 14. 某市为绿化环境计划植树2400棵,实际劳动中每天植树的数量比原计划多20%,结果提前8天完成任务.若设原计划每天植树x棵,则根据题意可列方程为 .15. 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,AB=12 ,OP=6,则劣弧AB的长为 .
14. 某市为绿化环境计划植树2400棵,实际劳动中每天植树的数量比原计划多20%,结果提前8天完成任务.若设原计划每天植树x棵,则根据题意可列方程为 .15. 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,AB=12 ,OP=6,则劣弧AB的长为 .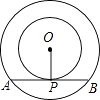 16. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.
16. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.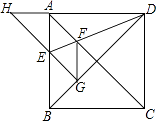
则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是 .
三、解答题
-
17. 解不等式组解不等式组 ,并把它的解集表示在数轴上.18. 如图,四边形ABCD中,AB∥CD,∠B=∠D,BC=6,AB=3,求四边形ABCD的周长.
 19. 某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:
19. 某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表:小组
研究报告
小组展示
答辩
甲
91
80
78
乙
81
74
85
丙
79
83
90
(1)、计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;(2)、如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高?20. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.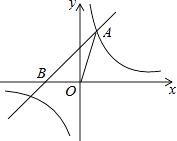 (1)、求k和b的值;(2)、求△OAB的面积.21. 已知△ABC中,∠A=90°.
(1)、求k和b的值;(2)、求△OAB的面积.21. 已知△ABC中,∠A=90°.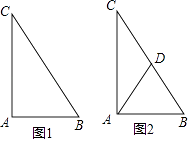 (1)、请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(1)、请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(2)、如图2,设BC边上的中线为AD,求证:BC=2AD.22. 如图①,②分别是某吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角. 吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A距地面的高度是多少米?(精确到0.1米. 参考数据:sin10°=cos80°≈0.17,cos10°=sin80°≈0.98,sin20°=cos70°≈0.34,tan70°≈2.75,sin70°≈0.94)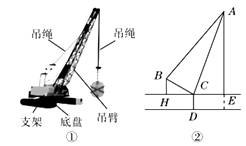 23. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
23. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.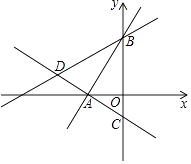 (1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求点D的坐标.24.
(1)、求线段BC的长度;(2)、试问:直线AC与直线AB是否垂直?请说明理由;(3)、若点D在直线AC上,且DB=DC,求点D的坐标.24.如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
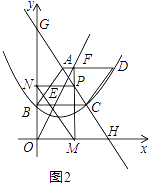
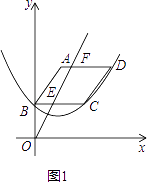 (1)、求抛物线的表达式;(2)、设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;(3)、
(1)、求抛物线的表达式;(2)、设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;(3)、如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
 25. 如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.
25. 如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.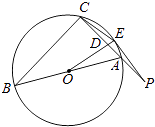 (1)、求证:△PAE∽△PEC;(2)、求证:PE为⊙O的切线;(3)、若∠B=30°,AP= AC,求证:DO=DP.
(1)、求证:△PAE∽△PEC;(2)、求证:PE为⊙O的切线;(3)、若∠B=30°,AP= AC,求证:DO=DP.