2019年广东省广州市中考数学模拟预测卷2

试卷更新日期：2019-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. 一种新型病毒的直径约为0.000043毫米，用科学记数法表示为（）毫米．

A、0.43×10^-4 B、0.43×10^-5 C、4.3×10^-5 D、4.3×10^-8

查看试题解析
2.
如图，将两个形状和大小都相同的杯子叠放在一起，则该实物图的主视图为（　　）

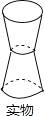A、 B、 C、 D、

查看试题解析
3. 如果a表示有理数，那么下列说法中正确的是（）

A、+a和﹣（﹣a）互为相反数 B、+a和﹣a一定不相等 C、﹣a一定是负数 D、﹣（+a）和+（﹣a）一定相等

查看试题解析
4. “抛一枚均匀硬币，落地后正面朝上”这一事件是（　　）

A、必然事件 B、随机事件 C、确定事件 D、不可能事件

查看试题解析
5. 已知分式 $\frac{(x - 1) (x + 2)}{x^{2} - 1}$ 的值为0，那么x的值是（）

A、﹣1 B、﹣2 C、1 D、1或﹣2

查看试题解析
6. 已知反比例函数y= $\frac{k}{x}$ 的图象如图所示，则二次函数y=﹣kx²﹣2x+ $\frac{k^{2}}{4}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
7.
如图Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为（　　）

A、2 $\sqrt{5}$ B、2 $\sqrt{3}$ C、2 $\sqrt{5}$ +2 D、2 $\sqrt{3}$ +2

查看试题解析
8. 若一次函数y=ax+b的图象经过第一、二、四象限，则下列不等式中总是成立的是（）

A、ab＞0 B、a﹣b＞0 C、a²+b＞0 D、a+b＞0

查看试题解析
9. 函数y=x²+bx+c与y=x的图象如图所示，有以下结论：
①b²﹣4c＞0；
②b+c+1=0；
③3b+c+6=0；
④当1＜x＜3时，x²+（b﹣1）x+c＜0．
其中正确的个数为（）

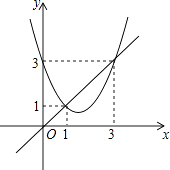A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是 $\frac{1}{x}$ ，矩形的周长是2（x+ $\frac{1}{x}$ ）；当矩形成为正方形时，就有x= $\frac{1}{x}$ （x＞0），解得x=1，这时矩形的周长2（x+ $\frac{1}{x}$ ）=4最小，因此x+ $\frac{1}{x}$ （x＞0）的最小值是2．模仿张华的推导，你求得式子 $\frac{x^{2} + 9}{x}$ （x＞0）的最小值是（　　）

A、2 B、1 C、6 D、10

查看试题解析

二、填空题

11. 分解因式：x²+xy= ．

查看试题解析
12.
化简：＝．

查看试题解析
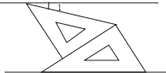
13.
如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是．

查看试题解析
14. 若代数式 $\frac{1}{x - 2}$ 和 $\frac{3}{2 x + 1}$ 的值相等，则x= ．

查看试题解析
15. 如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为 $\hat{A B}$ 的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为 cm² ．

查看试题解析
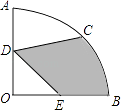16. 如图，矩形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，若AB=4，BC=6，则FD的长为．

查看试题解析

三、解答题

17. 解不等式（组）：

(1)、7x-2≤9x+2

(2)、 ${\begin{matrix} \frac{x - 2}{5} < 0 \\ 2 (2 x - 5) \leq 3 (4 x + 2) \end{matrix}$

查看试题解析
18. 已知：▱ABCD中，AB=5，AD=2，∠DAB=120°，若以点A为原点，直线AB为x轴，如图所示建立直角坐标系，试分别求出B、C、D三点的坐标．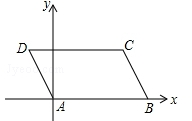

查看试题解析
19. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，获得如下不完整的统计图．
根据以上信息，解答下列问题：

(1)、问这次被抽检的电动汽车共有几辆？

(2)、补全条形统计图，并求出C等级对应的圆心角度数．

(3)、估计这种电动汽车一次充电后行驶的平均里程数为多少千米？

查看试题解析
20. 已知反比例函数y= $\frac{k - 1}{x}$ （k为常数，k≠1）
（1）其图象与正比例函数y=x的图象的一个交点为P，若点P的纵坐标是2，求k的值；
（2）若在其图象的每一支上，y随x的增大而减小，求k的取值范围．

查看试题解析
21. 如图，在Rt△ABC中，∠C=90°，∠B=30°．

(1)、用直尺和圆规作⊙O，使圆心O在BC边，且⊙O经过A，B两点上(不写作法，保留作图痕迹)；

(2)、连接A0，求证：AO平分∠CAB．

查看试题解析
22. 如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取 $\sqrt{3} \approx 1.732$ ，计算结果保留一位小数）

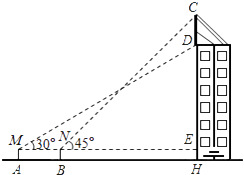(1)、求这幢大楼的高DH；

(2)、求这块广告牌CD的高度．

查看试题解析
23.
如图，一次函数y=ax+b的图象与反比例函数y= $\frac{k}{x}$ 的图象交于A，B两点，与x轴交于点C，与y轴交于点D，已知OA= $\sqrt{10}$ ， tan∠AOC= $\frac{1}{3}$ ，点B的坐标为（m，﹣2）．
（1）反比例函数的解析式．
（2）在y轴上存在一点，使得△PDC与△ODC相似，请你求出点P的坐标．

查看试题解析
24.
如图，抛物线y=ax²+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，对称轴与抛物线相交于点P、与直线BC相交于点M，连接PB．
（1）求该抛物线的解析式；
（2）抛物线上是否存在一点Q，使△QMB与△PMB的面积相等？若存在，求点Q的坐标；若不存在，说明理由；
（3）在第一象限、对称轴右侧的抛物线上是否存在一点R，使△RPM与△RMB的面积相等？若存在，直接写出点R的坐标；若不存在，说明理由．

查看试题解析
25.
如图，PB为⊙O的切线，B为切点，直线PO交⊙于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO与⊙O交于点C，连接BC，AF．

（1）求证：直线PA为⊙O的切线；
（2）试探究线段EF，OD，OP之间的等量关系，并加以证明；
（3）若BC＝6，tan∠F＝ $\frac{1}{2}$ ，求cos∠ACB的值和线段PE的长．

查看试题解析