2019年广东省广州市中考数学模拟预测卷1
试卷更新日期:2019-05-09 类型:中考模拟
一、选择题
-
1. 下列各数中,比-2小的数是( )A、2 B、0 C、-1 D、-32. 如图所示正三棱柱的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. ﹣23表示的意义是( ).A、(﹣2)×(﹣2)×(﹣2) B、(﹣2)+(﹣2)+(﹣2) C、(﹣2)×3 D、﹣2×2×24. A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )A、1 B、 C、 D、5. ÷ 化简结果为( ).A、 B、 C、 D、6. 如图3,直线y=-x与双曲线相交于A(-2,1)、B两点,则点B坐标为( )
3. ﹣23表示的意义是( ).A、(﹣2)×(﹣2)×(﹣2) B、(﹣2)+(﹣2)+(﹣2) C、(﹣2)×3 D、﹣2×2×24. A、B、C、D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若A首先抽签,则A抽到1号跑道的概率是( )A、1 B、 C、 D、5. ÷ 化简结果为( ).A、 B、 C、 D、6. 如图3,直线y=-x与双曲线相交于A(-2,1)、B两点,则点B坐标为( )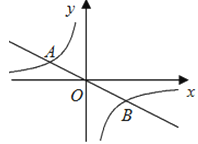 A、(2,-1) B、(1,-2) C、(1,) D、( , -1)7. 在ΔABC中∠B=90°,两直角边AB=7,BC=24,在三角形内有一点P到各边的距离相等,则这个距离是( )
A、(2,-1) B、(1,-2) C、(1,) D、( , -1)7. 在ΔABC中∠B=90°,两直角边AB=7,BC=24,在三角形内有一点P到各边的距离相等,则这个距离是( )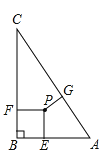 A、1 B、3 C、6 D、非以上答案8. 已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1 , y2 . 若y1≠y2 , 取y1 , y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2 , 此时M=﹣3.下列判断中:
A、1 B、3 C、6 D、非以上答案8. 已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数的图象的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1 , y2 . 若y1≠y2 , 取y1 , y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2 , 此时M=﹣3.下列判断中:①当x<0时,M=y1;
②当x>0时,M随x的增大而增大;
③使得M大于1的x值不存在;
④使得M=的值是﹣或 ,
其中正确的个数有( )
 A、1 B、2 C、3 D、410. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则的值为( )A、 B、99! C、9900 D、2!
A、1 B、2 C、3 D、410. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则的值为( )A、 B、99! C、9900 D、2!二、填空题
-
11. 分解因式:a2b+2ab2+b3= .12. 计算:( + )× = . .13.
如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC′= .
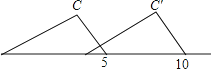 14. 若分式方程 的解为正数,则a的取值范围是 .15. 如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).随着点M的转动,当m从 变化到 时,点N相应移动的路径长为 .
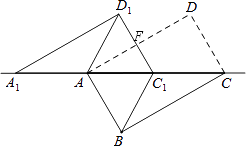
14. 若分式方程 的解为正数,则a的取值范围是 .15. 如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).随着点M的转动,当m从 变化到 时,点N相应移动的路径长为 .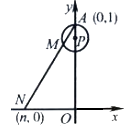 16. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连接AD1、BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
16. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1 , 连接AD1、BC1 . 若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:①△A1AD1≌△CC1B;
②当x=1时,四边形ABC1D1是菱形;
③当x=2时,△BDD1为等边三角形;
④S= (x﹣2)2(0≤x≤2).
其中正确的是(将所有正确答案的序号都填写在横线上)
三、解答题
-
17. 为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍?18.
图1,图2都是8×8的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点
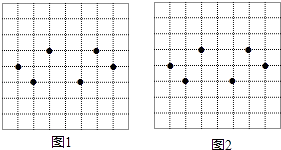 (1)、请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);(2)、图1中所画的平行四边形的面积为 .19. 某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)
(1)、请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);(2)、图1中所画的平行四边形的面积为 .19. 某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)
请根据图中提供的信息,回答下列问题:
(1)、α= , 并写出该扇形所对圆心角的度数为 , 请补全条形图 .(2)、在这次抽样调查中,众数和中位数分别是多少?(3)、如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?20. 在平面直角坐标系中,点A(﹣3,4)关于y轴的对称点为点B,连接AB,反比例函数y= (x>0)的图像经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ. (1)、点B的坐标是;k的值为(2)、判断△QDC与△POD的面积是否相等,并说明理由.21. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.
(1)、点B的坐标是;k的值为(2)、判断△QDC与△POD的面积是否相等,并说明理由.21. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.
(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.22. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60) 23. 如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A( , ),点D的坐标为(0,1)
23. 如图,在平面直角坐标系xOy中,直线y=﹣x+3与x轴交于点C,与直线AD交于点A( , ),点D的坐标为(0,1)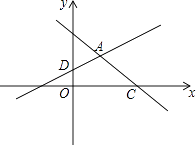 (1)、求直线AD的解析式;(2)、直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.24. 如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ x+b与抛物线的另一交点为D,且点D的横坐标为﹣5.
(1)、求直线AD的解析式;(2)、直线AD与x轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.24. 如图,已知抛物线y=a(x+2)(x﹣4)(a为常数,且a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣ x+b与抛物线的另一交点为D,且点D的横坐标为﹣5. (1)、求抛物线的函数表达式;(2)、P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;(3)、设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?25. 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
(1)、求抛物线的函数表达式;(2)、P为直线BD下方的抛物线上的一点,连接PD、PB,求△PBD面积的最大值;(3)、设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?25. 如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC (1)、求CD的长;(2)、求证:PC是⊙O的切线;(3)、点G为 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.
(1)、求CD的长;(2)、求证:PC是⊙O的切线;(3)、点G为 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.