安徽省黄山市2019届高中毕业班数学第二次质量检测试卷

试卷更新日期：2019-05-09 类型：高考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题5分，共60分。）

1. 已知复数z满足z（1+i）=3+4i，则复数z在复平面内表示的点所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知x∈（0， $\frac{π}{2}$ ），cos（x+ $\frac{π}{4}$ ）= $\frac{3}{5}$ ，则sinx的值为（）

A、- $\frac{\sqrt{2}}{10}$ B、 $\frac{\sqrt{2}}{10}$ C、 $\frac{7 \sqrt{2}}{10}$ D、- $\frac{7 \sqrt{2}}{10}$

查看试题解析
3. 已知a= $\int_{0}^{π} \sin x d x$ ，则（x- $\frac{a}{x}$ ）⁵展开式中x^-1项的系数为（）

A、10 B、-10 C、80 D、-80

查看试题解析
4. 已知双曲线 $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$ 的左焦点为F₁ ，过F₁的直线l交双曲线左支于A、B两点，则l斜率的范围为（）

A、（- $\frac{4}{3}$ ， $\frac{4}{3}$ ） B、（-∞，- $\frac{3}{4}$ ）U（ $\frac{3}{4}$ ，+∞） C、（- $\frac{3}{4}$ ， $\frac{3}{4}$ ） D、（-∞，- $\frac{4}{3}$ ）U（ $\frac{4}{3}$ ，+∞）

查看试题解析
5. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{a}$ |=2，| $\vec{b}$ |= $\sqrt{2}$ ，且 $\vec{a}$ ⊥（ $\vec{a}$ +2 $b$ ），则 $\vec{b}$ 在 $\vec{a}$ 方向上的投影为（）

A、1 B、-1 C、 $\sqrt{2}$ D、- $\sqrt{2}$

查看试题解析
6. 已知f（x）=Asin（ωx+φ）+B（A>0，ω>0，|φ|< $\frac{π}{2}$ ）部分图象如图，则f（x）的一个对称中心是（）

A、（π，0） B、（ $\frac{π}{12}$ ，0） C、（- $\frac{5 π}{6}$ ，-1） D、（- $\frac{π}{6}$ ，-1）

查看试题解析
7. 在《九章算术》中，将四个面都是直角三角形的四面体称为鳖膈，在鳖膈A-BCD中，AB⊥平面BCD，BC⊥CD，且AB=BC=CD，M为AD的中点，则异面直线BM与CD夹角的余弦值为（）

A、 $\frac{\sqrt{2}}{3}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2}}{4}$

查看试题解析
8. 设a>0且a≠1，则“b>a”是“log_ab>1”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
9. 某空间几何体的三视图如图所示，其中正视图和俯视图均为边长为1的等腰直角三角形，则此空间几何体的表面积是（）

A、 $\sqrt{2} + \frac{\sqrt{3}}{2}$ B、 $1 + \frac{\sqrt{3}}{2}$ C、 $\sqrt{2} + \frac{\sqrt{3} + 1}{2}$ D、 $\sqrt{2} + \sqrt{3}$

查看试题解析
10. 程序按图如图，若输入的a=2，则输出的结果为（）

A、 $\frac{2019}{2}$ B、1010 C、 $\frac{2023}{2}$ D、1012

查看试题解析
11. 将三颗做子各掷一次，设事件A=“三个点数互不相同”，B=“至多出现一个奇数”，则概率P（A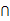 B）等于（）

A、 $\frac{1}{4}$ B、 $\frac{35}{36}$ C、 $\frac{5}{18}$ D、 $\frac{5}{12}$

查看试题解析
12. 已知定义在R上的连续可导函数f（x）无极值，且 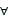x∈R，f[f（x）+2018^x]=2019，若g（x）=2sin（x+ $\frac{π}{6}$ ）+mx在[ $\frac{3 π}{2}$ ，2π]上与函数f（x）的单调性相同，则实数m的取值范围是（）

A、（-∞，-2] B、[-2，+∞） C、（-∞，2] D、[-2，-1]

查看试题解析

二、填空题（本大题共4小题，每小题5分，共20分。）

13. 若整数x、y满足不等式组 ${\begin{matrix} \begin{array}{l} 0 \leq x \leq 2 \\ x + y - 2 > 0 \end{array} \\ x - y + 2 > 0 \end{matrix}$ ，则z= $\frac{y}{x}$ 的最小值为.

查看试题解析
14. 已知椭圆C $\frac{x^{2}}{a^{2}} + y^{2} = 1$ （a>1）的焦点为F₁、F₂ ，以原点为圆心、椭圆的焦距为直径的⊙O与椭圆C交于点P，则△PF₁F₂=.

查看试题解析
15. 定义在R上的函数f（x）满足f（x）+f（-x）=0，若g（x）=f（x）cosx+1，且g（ln2）=-2，则g(ln $\frac{1}{2}$ ）=。

查看试题解析
16. 已知O是锐角△MBC的外接圆圆心，A是最大角，若 $\frac{\cos B}{\sin C} \vec{A B} + \frac{cosC}{sinB} \vec{A C} = m \vec{A O}$ ，则m的取值范围为。

查看试题解析

三、解答题（本大题共6小题，共70分）

17. 已知数列{a_n}满足， $\frac{1}{a_{1} - 1} + \frac{1}{a_{2} - 1} + \frac{1}{a_{3} - 1} + \dots + \frac{n}{a_{n} - 1} = n$ ，n∈N^*.
a.-1

（I）求数列{a_n}的通项公式；

（II）令b_n= $\frac{2 n + 1}{{(a_{n} - 1)}^{2} {(a_{n + 1} - 1)}^{2}}$ ，数列{b_n}的前n项和为T_n ，求证：T_n<1.

查看试题解析
18. 如图，已知四边形ABCD满足AD∥BC，BA=AD=DC= $\frac{1}{2}$ BC=a，E是BC的中点，将△BAE沿AE翻折成△B₁AE，使得B₁D= $\frac{\sqrt{6}}{2}$ a，F为B，D的中点

（I）证明：B₁E∥平面ACF；

（III）求平面ADB1与平面ECB₁所成锐二面角的余弦值。

查看试题解析

19. 某校为了解校园安全教育系列活动的成效，对全校学生进行一次安全意识测试，根据考试成绩评定“合格”、“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分，现随机抽取部分学生的成绩，统计结果及对应的频率分布直方图如下所示：

等级	不合格		合格
得分	[20，40）	[40，60）	[60，80）	[80，100]
频数	6	x	24	y

（I）若测试的同学中，分数段[20，40）、[40，60）、[60，80）、[80，100]内女生的人数分别为2人、8人、16人、4人，完成2×2列联表，并判断：是否有90%以上的充准认为性别与安全意识有关？

（II）用分层抽样的方法，从评定等级为“合格”和“不合格”的学生中，共选取10人进行座谈，现再从这10人中任选4人，记所选4人的量化总分为X，求X的分布列及数学期望E（X）；

（III）某评估机构以指标M（M= $\frac{E (X)}{D (X)}$ ，其中D（X）表示X的方差）来评估该校安全教育活动的成效。若M≥0.7，则认定教育活动是有效的；否则认定教育活动无效，应调整安全教育方案。在（II）的条件下，判断该校是否应调整安全教育方案？

附表及公式：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d.

P(K²≥k₀)	0.15	0.10	0.05	0.025	0.010
k₀	2.072	2.706	3.841	5.024	6.635

是否合格性别	不合格	合格	总计
男生
女生
总计

查看试题解析

20. 已知△ABC中，AB=2，且sin A（1-2cosB）+sinB（1-2cosA）=0以边AB的中垂线为x轴，以AB所在的直线为y轴，建立平面直角坐标系.
(I）求动点C的轨迹E的方程：

(II)已知定点P（0，4），不垂直于AB的动直线/与轨迹E相交于M、W两点，若直线MP、NP关于y轴对称，求△PMN面积的取值范围。

查看试题解析
21. 设函数f(x)= $\frac{a (x^{2} + 1)}{e^{x}}$ ，g(x)= $\frac{x}{e^{x}}$ ，
（I）求函数F（x）= $\frac{x + 2}{g (x)}$ 单调递减区间；

（II）若函数G（x）=f（x）+g（x）（a≤0）的极小值不小于- $\frac{2}{e^{2}}$ ，求实数a的取值范围。

查看试题解析
22. 设极坐标系与直角坐标系xOy有相同的长度单位，原点O为极点，x轴正半轴为极轴，曲线C的参数方程为 ${\begin{matrix} x = 1 + c o s α \\ y = s i n α \end{matrix}$ （α是参数），直线l的极坐标方程为 $\sqrt{3}$
psinθ-pcosθ+1= $\sqrt{3}$ m.

（I）求曲线C的普通方程和直线l的参数方程；

（II）设点P（1，m），若直线l与曲线C相交于A、B两点，且|PA|= $\frac{8}{| P B |}$ ，求m的值。

查看试题解析
23. 已知f（x）=|2-x|-|4-x|.

(1)、关于x的不等式f（x）≥a²-3a恒成立，求实数a的取值范围；
（II）若f（m）+f（n）=4，且m<n，求m+n的取值范围。

查看试题解析