2016年江苏省泰州市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、选择题：

1. 4的平方根是（）

A、±2 B、﹣2 C、2 D、 $\pm \frac{1}{2}$

查看试题解析
2. 人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为（）

A、77×10^﹣⁵ B、0.77×10^﹣⁷ C、7.7×10^﹣⁶ D、7.7×10^﹣⁷

查看试题解析
3. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示的几何体，它的左视图与俯视图都正确的是（）

A、 B、 C、 D、

查看试题解析
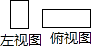5. 对于一组数据﹣1，﹣1，4，2，下列结论不正确的是（）

A、平均数是1 B、众数是﹣1 C、中位数是0.5 D、方差是3.5

查看试题解析
6. 实数a、b满足 $\sqrt{a + 1}$ +4a²+4ab+b²=0，则b^a的值为（）

A、2 B、 $\frac{1}{2}$ C、﹣2 D、﹣ $\frac{1}{2}$

查看试题解析

二、填空题：

7. （﹣ $\frac{1}{2}$ ）⁰等于．

查看试题解析
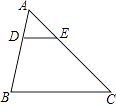
8. 函数 $\frac{1}{2 x - 3}$ 中，自变量x的取值范围是．

查看试题解析
9. 抛掷一枚质地均匀的正方体骰子1枚，朝上一面的点数为偶数的概率是．

查看试题解析
10. 五边形的内角和是°．

查看试题解析
11. 如图，△ABC中，D、E分别在AB、AC上，DE∥BC，AD：AB=1：3，则△ADE与△ABC的面积之比为．

查看试题解析
12. 如图，已知直线l₁∥l₂ ，将等边三角形如图放置，若∠α=40°，则∠β等于．

查看试题解析
13. 如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A′B′C′的对应位置时，A′B′恰好经过AC的中点O，则△ABC平移的距离为cm．

查看试题解析
14. 方程2x﹣4=0的解也是关于x的方程x²+mx+2=0的一个解，则m的值为．

查看试题解析
15. 如图，⊙O的半径为2，点A、C在⊙O上，线段BD经过圆心O，∠ABD=∠CDB=90°，AB=1，CD= $\sqrt{3}$ ，则图中阴影部分的面积为．

查看试题解析
16. 二次函数y=x²﹣2x﹣3的图象如图所示，若线段AB在x轴上，且AB为2 $\sqrt{3}$ 个单位长度，以AB为边作等边△ABC，使点C落在该函数y轴右侧的图象上，则点C的坐标为．

查看试题解析

三、解答题

17. 计算或化简：

(1)、 $\frac{1}{2}$ $\sqrt{12}$ ﹣（3 $\sqrt{\frac{1}{3}}$ + $\sqrt{2}$ ）；

(2)、（ $\frac{m}{m - 2}$ ﹣ $\frac{2 m}{m^{2} - 4}$ $\frac{2 m}{m^{2} - 4}$ ）÷ $\frac{m}{m + 2}$ ．

查看试题解析
18. 某校为更好地开展“传统文化进校园”活动，随机抽查了部分学生，了解他们最喜爱的传统文化项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题：

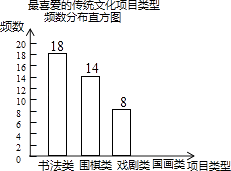(1)、直接写出频数分布表中a的值；

(2)、补全频数分布直方图；

(3)、若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？

查看试题解析
19. 一只不透明的袋子中装有3个球，球上分别标有数字0，1，2，这些球除了数字外其余都相同，甲、乙两人玩摸球游戏，规则如下：先由甲随机摸出一个球（不放回），再由乙随机摸出一个球，两人摸出的球所标的数字之和为偶数时则甲胜，和为奇数时则乙胜．

(1)、用画树状图或列表的方法列出所有可能的结果；

(2)、这样的游戏规则是否公平？请说明理由．

查看试题解析
20. 随着互联网的迅速发展，某购物网站的年销售额从2013年的200万元增长到2015年的392万元．求该购物网站平均每年销售额增长的百分率．

查看试题解析
21. 如图，△ABC中，AB=AC，E在BA的延长线上，AD平分∠CAE．

(1)、求证：AD∥BC；

(2)、过点C作CG⊥AD于点F，交AE于点G，若AF=4，求BC的长．

查看试题解析
22. 如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以6千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内．当该飞行器飞行至村庄C的正上方A处时，测得∠NAD=60°；该飞行器从A处飞行40分钟至B处时，测得∠ABD=75°．求村庄C、D间的距离（ $\sqrt{3}$ 取1.73，结果精确到0.1千米）

查看试题解析
23. 如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．

(1)、判断AB与⊙O的位置关系，并说明理由；

(2)、若PF：PC=1：2，AF=5，求CP的长．

查看试题解析
24. 如图，点A（m，4），B（﹣4，n）在反比例函数y= $\frac{k}{x}$ （k＞0）的图象上，经过点A、B的直线与x轴相交于点C，与y轴相交于点D．

(1)、若m=2，求n的值；

(2)、求m+n的值；

(3)、连接OA、OB，若tan∠AOD+tan∠BOC=1，求直线AB的函数关系式．

查看试题解析
25.
已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．

(1)、如图1，若点P在线段AB的延长线上，求证：EA=EC；

(2)、若点P在线段AB上．
①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；
②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．

查看试题解析
26. 已知两个二次函数y₁=x²+bx+c和y₂=x²+m．对于函数y₁ ，当x=2时，该函数取最小值．

(1)、求b的值；

(2)、若函数y₁的图象与坐标轴只有2个不同的公共点，求这两个公共点间的距离；

(3)、若函数y₁、y₂的图象都经过点（1，﹣2），过点（0，a﹣3）（a为实数）作x轴的平行线，与函数y₁、y₂的图象共有4个不同的交点，这4个交点的横坐标分别是x₁、x₂、x₃、x₄ ，且x₁＜x₂＜x₃＜x₄ ，求x₄﹣x₃+x₂﹣x₁的最大值．

查看试题解析

项目类型	频数	频率
书法类	18	a
围棋类	14	0.28
喜剧类	8	0.16
国画类	b	0.20