2014年江苏省镇江市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、填空题

1. 计算：|﹣5|= ．

查看试题解析
2. 计算：（﹣ $\frac{1}{3}$ ）×3= ．

查看试题解析
3. 化简：（x+1）（x﹣1）+1= ．

查看试题解析
4. 分式 $\frac{2}{x - 1}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
5. 如图，CD是△ABC的中线，点E、F分别是AC、DC的中点，EF=1，则BD= ．

查看试题解析
6. 如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90°．若∠1=25°，∠2=70°，则∠B= ．

查看试题解析
7. 一组数据：1，2，1，0，2，a，若它们众数为1，则这组数据的平均数为．

查看试题解析
8. 若关于x的一元二次方程x²+x+m=0有两个相等的实数根，则m= ．

查看试题解析
9. 已知圆锥的底面半径为3，母线长为8，则圆锥的侧面积等于．

查看试题解析
10. 如图，将△OAB绕着点O逆时针连续旋转两次得到△OA″B″，每次旋转的角度都是50°．若∠B″OA=120°，则∠AOB= ．

查看试题解析
11. 一辆货车从甲地匀速驶往乙地，到达后用了半小时卸货，随即匀速返回，已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍．货车离甲地的距离y（千米）关于时间x（小时）的函数图象如图所示．则a=（小时）．

查看试题解析
12. 读取表格中的信息，解决问题．
n=1
a₁= $\sqrt{2}$ +2 $\sqrt{3}$
b₁= $\sqrt{3}$ +2
c₁=1+2 $\sqrt{2}$
n=2
a₂=b₁+2c₁
b₂=c₁+2a₁
c₂=a₁+2b₁
n=3
a₃=b₂+2c₂
b₃=c₂+2a₂
c=a₂+2b₂
…
…
…
…
满足 $\frac{a_{n} + b_{n} + c_{n}}{\sqrt{3} + \sqrt{2}} \geq 2014 \times (\sqrt{3} - \sqrt{2} + 1)$ 的n可以取得的最小整数是．

查看试题解析

二、选择题

13. 下列运算正确的是（）

A、（x³）³=x⁹ B、（﹣2x）³=﹣6x³ C、2x²﹣x=x D、x⁶÷x³=x²

查看试题解析
14. 一个圆柱如图放置，则它的俯视图是（）

A、三角形 B、半圆 C、圆 D、矩形

查看试题解析
15. 若实数x、y满足 $\sqrt{2 x - 1} + 2 {(y - 1)}^{2}$ =0，则x+y的值等于（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
16. 如图，△ABC内接于半径为5的⊙O，圆心O到弦BC的距离等于3，则∠A的正切值等于（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
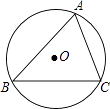17. 已知过点（2，﹣3）的直线y=ax+b（a≠0）不经过第一象限，设s=a+2b，则s的取值范围是（）

A、﹣5≤s≤﹣ $\frac{3}{2}$ B、﹣6＜s≤﹣ $\frac{3}{2}$ C、﹣6≤s≤﹣ $\frac{3}{2}$ D、﹣7＜s≤﹣ $\frac{3}{2}$

查看试题解析

三、解答题

18.

(1)、计算：（ $\frac{1}{2}$ ）^﹣¹+ $\sqrt{2}$ cos45°﹣ $\sqrt[3]{27}$ ；

(2)、化简：（x+ $\frac{1}{x - 2}$ ）÷ $\frac{x - 1}{3 x - 6}$ ．

查看试题解析
19.

(1)、解方程： $\frac{3}{x}$ ﹣ $\frac{2}{x + 2}$ =0；

(2)、解不等式：2+ $\frac{2 x - 1}{3}$ ≤x，并将它的解集在数轴上表示出来．

查看试题解析
20. 如图，在四边形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，点E在AO上，且OE=OC．

(1)、求证：∠1=∠2；

(2)、连结BE、DE，判断四边形BCDE的形状，并说明理由．

查看试题解析
21. 为了了解“通话时长”（“通话时长”指每次通话时间）的分布情况，小强收集了他家1000个“通话时长”数据，这些数据均不超过18（分钟）．他从中随机抽取了若干个数据作为样本，统计结果如下表，并绘制了不完整的频数分布直方图．
“通话时长”
（x分钟）
0＜x≤3
3＜x≤6
6＜x≤9
9＜x≤12
12＜x≤15
15＜x≤18
次数
36
a
8
12
8
12
根据表、图提供的信息，解答下面的问题：

(1)、a= ，样本容量是；

(2)、求样本中“通话时长”不超过9分钟的频率：；

(3)、请估计小强家这1000次通话中“通话时长”超过15分钟的次数．

查看试题解析
22. 在一只不透明的布袋中装有红球、黄球各若干个，这些球除颜色外都相同，充分摇匀．

(1)、若布袋中有3个红球，1个黄球．从布袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）；

(2)、若布袋中有3个红球，x个黄球．
请写出一个x的值，使得事件“从布袋中一次摸出4个球，都是黄球”是不可能的事件；

(3)、若布袋中有3个红球，4个黄球．
我们知道：“从袋中一次摸出4个球，至少有一个黄球”为必然事件．
请你仿照这个表述，设计一个必然事件：．

查看试题解析
23. 在平面直角坐标系xOy中，直线y=kx+4（k≠0）与y轴交于点A．

(1)、如图，直线y=﹣2x+1与直线y=kx+4（k≠0）交于点B，与y轴交于点C，点B的横坐标为﹣1．
①求点B的坐标及k的值；
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于；

(2)、直线y=kx+4（k≠0）与x轴交于点E（x₀ ， 0），若﹣2＜x₀＜﹣1，求k的取值范围．

查看试题解析
24.
如图，小明从点A处出发，沿着坡角为α的斜坡向上走了0.65千米到达点B，sinα= $\frac{5}{13}$ ，然后又沿着坡度为i=1：4的斜坡向上走了1千米达到点C．问小明从A点到点C上升的高度CD是多少千米（结果保留根号）？

查看试题解析
25. 六•一儿童节，小文到公园游玩．看到公园的一段人行弯道MN（不计宽度），如图，它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN（MP⊥OP，NQ⊥OQ），他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等，比如：A、B、C是弯道MN上的三点，矩形ADOG、矩形BEOH、矩形CFOI的面积相等．爱好数学的他建立了平面直角坐标系（如图），图中三块阴影部分的面积分别记为S₁、S₂、S₃ ，并测得S₂=6（单位：平方米）．OG=GH=HI．

(1)、求S₁和S₃的值；

(2)、设T（x，y）是弯道MN上的任一点，写出y关于x的函数关系式；

(3)、公园准备对区域MPOQN内部进行绿化改造，在横坐标、纵坐标都是偶数的点处种植花木（区域边界上的点除外），已知MP=2米，NQ=3米．问一共能种植多少棵花木？

查看试题解析
26. 如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．

(1)、求证：EA是⊙O的切线；

(2)、已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；

(3)、已知AF=4，CF=2．在（2）条件下，求AE的长．

查看试题解析
27.
如图1，在平面直角坐标系xOy中，点M为抛物线y=﹣x²+2nx﹣n²+2n的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．

(1)、求抛物线的函数关系式，并写出点P的坐标；

(2)、小丽发现：将抛物线y=﹣x²+2nx﹣n²+2n绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗？请说明理由；

(3)、如图2，已知点A（1，0），以PA为边作矩形PABC（点P、A、B、C按顺时针的方向排列）， $\frac{P A}{A B} = \frac{1}{t}$ ．
写出C点的坐标：C（，）（坐标用含有t的代数式表示）；

(4)、
若点C在题（2）中旋转后的新抛物线上，求t的值．

查看试题解析
28. 我们知道平行四边形那有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论

(1)、【发现与证明】
在▱ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连接B′D．
结论1：B′D∥AC；
结论2：△AB′C与▱ABCD重叠部分的图形是等腰三角形．
…
请利用图1证明结论1或结论2．

(2)、
【应用与探究】
在▱ABCD中，∠B=30°，将△ABC沿AC翻折至△AB′C，连接B′D．
如图1，若AB= $\sqrt{3}$ ，∠AB′D=75°，则∠ACB= ， BC=；

(3)、
如图2，AB=2 $\sqrt{3}$ ，BC=1，AB′与CD相交于点E，求△AEC的面积；

(4)、已知AB=2 $\sqrt{3}$ ，当BC的长为多少时，△AB′D是直角三角形？

查看试题解析

n=1	a₁= $\sqrt{2}$ +2 $\sqrt{3}$	b₁= $\sqrt{3}$ +2	c₁=1+2 $\sqrt{2}$
n=2	a₂=b₁+2c₁	b₂=c₁+2a₁	c₂=a₁+2b₁
n=3	a₃=b₂+2c₂	b₃=c₂+2a₂	c=a₂+2b₂
…	…	…	…