2014年江苏省徐州市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、选择题

1. 2^﹣¹等于（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 如图是用五个相同的立方块搭成的几何体，其主视图是（）

A、 B、 C、 D、

查看试题解析
3. 抛掷一枚均匀的硬币，前2次都正面朝上，第3次正面朝上的概率（）

A、大于 $\frac{1}{2}$ B、等于 $\frac{1}{2}$ C、小于 $\frac{1}{2}$ D、不能确定

查看试题解析
4. 下列运算中错误的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{2}$ × $\sqrt{3}$ = $\sqrt{6}$ C、 $\sqrt{8}$ ÷ $\sqrt{2}$ =2 D、 ${(- \sqrt{3})}^{2}$ =3

查看试题解析
5. 将函数y=﹣3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为（）

A、y=﹣3x+2 B、y=﹣3x﹣2 C、y=﹣3（x+2） D、y=﹣3（x﹣2）

查看试题解析
6. 顺次连接正六边形的三个不相邻的顶点．得到如图所示的图形，该图形（）

A、既是轴对称图形也是中心对称图形 B、是轴对称图形但并不是中心对称图形 C、是中心对称图形但并不是轴对称图形 D、既不是轴对称图形也不是中心对称图形

查看试题解析
7. 若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（）

A、矩形 B、等腰梯形 C、对角线相等的四边形 D、对角线互相垂直的四边形

查看试题解析
8. 点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于（）

A、3 B、2 C、3或5 D、2或6

查看试题解析

二、填空题

9. 函数y= $\frac{2}{x - 1}$ 中，自变量x的取值范围为．

查看试题解析
10. 我国“钓鱼岛”周围海域面积约170 000km² ，该数用科学记数法可表示为．

查看试题解析
11. 函数y=2x与y=x+1的图象的交点坐标为．

查看试题解析
12. 若ab=2，a﹣b=﹣1，则代数式a²b﹣ab²的值等于．

查看试题解析
13. 半径为4cm，圆心角为60°的扇形的面积为cm² ．

查看试题解析
14. 如图是某足球队全年比赛情况统计图：
根据图中信息，该队全年胜了场．

查看试题解析
15. 在平面直角坐标系中，将点A（4，2）绕原点逆时针方向旋转90°后，其对应点A′的坐标为．

查看试题解析
16. 如图，在等腰三角形纸片ABC中，AB=AC，∠A=50°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE=°．

查看试题解析
17. 如图，以O为圆心的两个同心圆中，大圆与小圆的半径分别为3cm和1cm，若⊙P与这两个圆都相切，则圆P的半径为cm．

查看试题解析
18.
如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发xs时，△PAQ的面积为ycm² ， y与x的函数图象如图②，则线段EF所在的直线对应的函数关系式为．

查看试题解析

三、解答题

19.

(1)、计算：（﹣1）²+sin30°﹣ $\sqrt[3]{8}$ ；

(2)、计算：（a+ $\frac{1}{a - 2}$ ）÷（1+ $\frac{1}{a - 2}$ ）．

查看试题解析
20.

(1)、解方程：x²+4x﹣1=0；

(2)、解不等式组： ${\begin{matrix} - 2 x \leq 0 \\ 3 x - 1 < 5 \end{matrix}$ ．

查看试题解析
21. 已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=CF．
求证：四边形BEDF是平行四边形．

查看试题解析
22. 甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9

(1)、填写下表：
平均数
众数
中位数
方差
甲
8
8
0.4
乙
9
3.2

(2)、教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？

(3)、如果乙再射击1次，命中8环，那么乙的射击成绩的方差．（填“变大”、“变小”或“不变”）．

查看试题解析
23. 某学习小组由3名男生和1名女生组成，在一次合作学习后，开始进行成果展示．

(1)、如果随机抽取1名同学单独展示，那么女生展示的概率为；

(2)、如果随机抽取2名同学共同展示，求同为男生的概率．

查看试题解析
24. 几个小伙伴打算去音乐厅观看演出，他们准备用360元钱购买门票．下面是两个小伙伴的对话：
根据对话的内容，请你求出小伙伴们的人数．

查看试题解析
25.
如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．

(1)、求点C与点A的距离（精确到1km）；

(2)、确定点C相对于点A的方向．
（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
26. 某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax²+bx﹣75．其图象如图所示．

(1)、销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？

(2)、销售单价在什么范围时，该种商品每天的销售利润不低于16元？

查看试题解析
27.
如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数y= $\frac{k}{x}$ 图象的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F．已知B（1，3）．

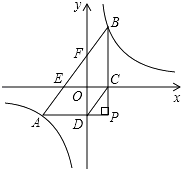(1)、k=；

(2)、试说明AE=BF；

(3)、当四边形ABCD的面积为 $\frac{21}{4}$ 时，求点P的坐标．

查看试题解析
28. 如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

(1)、试说明四边形EFCG是矩形；

(2)、当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．

查看试题解析

	平均数	众数	中位数	方差
甲	8		8	0.4
乙		9		3.2