2014年江苏省宿迁市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、选择题

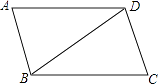
1. ﹣3的相反数是（）

A、3 B、 $\frac{1}{3}$ C、﹣ $\frac{1}{3}$ D、﹣3

查看试题解析
2. 下列计算正确的是（）

A、a³+a⁴=a⁷ B、a³•a⁴=a⁷ C、a⁶÷a³=a² D、（a³）⁴=a⁷

查看试题解析
3. 如图，▱ABCD中，BC=BD，∠C=74°，则∠ADB的度数是（）

A、16° B、22° C、32° D、68°

查看试题解析
4. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是方程组 ${\begin{cases} a x + b y = 5 \\ b x + a y = 1 \end{cases}$ 的解，则a﹣b的值是（）

A、﹣1 B、2 C、3 D、4

查看试题解析
5. 若一个圆锥的主视图是腰长为5，底边长为6的等腰三角形，则该圆锥的侧面积是（）

A、15π B、20π C、24π D、30π

查看试题解析
6. 一只不透明的袋子中装有两个完全相同的小球，上面分别标有1，2两个数字，若随机地从中摸出一个小球，记下号码后放回，再随机摸出一个小球，则两次摸出小球的号码之积为偶数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
7. 若将抛物线y=x²向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（）

A、y=（x+2）²+3 B、y=（x﹣2）²+3 C、y=（x+2）²﹣3 D、y=（x﹣2）²﹣3

查看试题解析
8. 如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，则满足条件的点P的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 已知实数a，b满足ab=3，a﹣b=2，则a²b﹣ab²的值是．

查看试题解析
10. 不等式组 ${\begin{matrix} 2 x - 1 > 1 \\ 3 - x > 1 \end{matrix}$ 的解集是．

查看试题解析
11. 某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是分．

查看试题解析
12. 一块矩形菜地的面积是120m² ，如果它的长减少2m，那么菜地就变成正方形，则原菜地的长是m．

查看试题解析
13. 如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是．

查看试题解析
14. 如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是．

查看试题解析
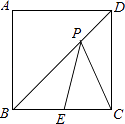15. 如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC与BC相交于点D，若AD=4，CD=2，则AB的长是．

查看试题解析
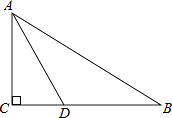16. 如图，一次函数y=kx﹣1的图象与x轴交于点A，与反比例函数y= $\frac{3}{x}$ （x＞0）的图象交于点B，BC垂直x轴于点C．若△ABC的面积为1，则k的值是．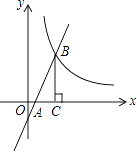

查看试题解析

三、解答题

17. 计算：2sin30°+|﹣2|+（ $\sqrt{2}$ ﹣1）⁰﹣ $\sqrt{4}$ ．

查看试题解析
18. 解方程： $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$ ．

查看试题解析
19. 为了了解某市初三年级学生体育成绩（成绩均为整数），随机抽取了部分学生的体育成绩并分段（A：20.5～22.5；B：22.5～24.5；C：24.5～26.5；D：26.5～28.5；E：28.5～30.5）统计如下体育成绩统计表
分数段
频数/人
频率
A
12
0.05
B
36
a
C
84
0.35
D
b
0.25
E
48
0.20
根据上面提供的信息，回答下列问题：

(1)、在统计表中，a= ， b= ，并将统计图补充完整；

(2)、小明说：“这组数据的众数一定在C中．”你认为小明的说法正确吗？（填“正确”或“错误”）；

(3)、若成绩在27分以上（含27分）定为优秀，则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少？

查看试题解析
20. 如图是两个全等的含30°角的直角三角形．

(1)、将其相等边拼在一起，组成一个没有重叠部分的平面图形，请你画出所有不同的拼接平面图形的示意图；

(2)、若将（1）中平面图形分别印制在质地、形状、大小完全相同的卡片上，洗匀后从中随机抽取一张，求抽取的卡片上平面图形为轴对称图形的概率．

查看试题解析
21. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径为 $\sqrt{5}$ ，OP=1，求BC的长．

查看试题解析
22. 如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．

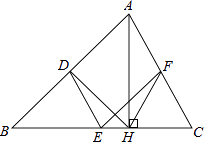(1)、求证：四边形ADEF是平行四边形；

(2)、求证：∠DHF=∠DEF．

查看试题解析
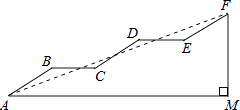
23.
如图是某通道的侧面示意图，已知AB∥CD∥EF，AM∥BC∥DE，AB=CD=EF，∠AMF=90°，∠BAM=30°，AB=6m．

(1)、求FM的长；

(2)、连接AF，若sin∠FAM= $\frac{1}{3}$ ，求AM的长．

查看试题解析
24. 如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=8cm．BC=4cm，CD=5cm．动点P从点B开始沿折线BC﹣CD﹣DA以1cm/s的速度运动到点A．设点P运动的时间为t（s），△PAB面积为S（cm²）．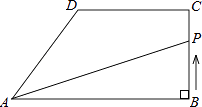

(1)、当t=2时，求S的值；

(2)、当点P在边DA上运动时，求S关于t的函数表达式；

(3)、当S=12时，求t的值．

查看试题解析
25. 如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．

(1)、当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

(2)、将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；

(3)、将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

查看试题解析
26. 如图，已知抛物线y=ax²+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．

(1)、
如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的表达式与点D的坐标；
②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；

(2)、
如图2，若a=1，求证：无论b，c取何值，点D均为定点，求出该定点坐标．

查看试题解析

分数段	频数/人	频率
A	12	0.05
B	36	a
C	84	0.35
D	b	0.25
E	48	0.20