2014年江苏省无锡市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的相反数是（）

A、3 B、﹣3 C、±3 D、 $\frac{1}{3}$

查看试题解析
2. 函数y= $\sqrt{2 - x}$ 中自变量x的取值范围是（）

A、x＞2 B、x≥2 C、x≤2 D、x≠2

查看试题解析
3. 分式 $\frac{2}{2 - x}$ 可变形为（）

A、 $\frac{2}{2 + x}$ B、﹣ $\frac{2}{2 + x}$ C、 $\frac{2}{x - 2}$ D、﹣ $\frac{2}{x - 2}$

查看试题解析
4. 已知A样本的数据如下：72，73，76，76，77，78，78，78，B样本的数据恰好是A样本数据每个都加2，则A，B两个样本的下列统计量对应相同的是（）

A、平均数 B、标准差 C、中位数 D、众数

查看试题解析
5. 某文具店一支铅笔的售价为1.2元，一支圆珠笔的售价为2元．该店在“6•1儿童节”举行文具优惠售卖活动，铅笔按原价打8折出售，圆珠笔按原价打9折出售，结果两种笔共卖出60支，卖得金额87元．若设铅笔卖出x支，则依题意可列得的一元一次方程为（）

A、1.2×0.8x+2×0.9（60+x）=87 B、1.2×0.8x+2×0.9（60﹣x）=87 C、2×0.9x+1.2×0.8（60+x）=87 D、2×0.9x+1.2×0.8（60﹣x）=87

查看试题解析
6. 已知圆锥的底面半径为4cm，母线长为5cm，则这个圆锥的侧面积是（）

A、20πcm² B、20cm² C、40πcm² D、40cm²

查看试题解析
7. 如图，AB∥CD，则根据图中标注的角，下列关系中成立的是（）

A、∠1=∠3 B、∠2+∠3=180° C、∠2+∠4＜180° D、∠3+∠5=180°

查看试题解析
8. 如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A=30°，给出下面3个结论：①AD=CD；②BD=BC；③AB=2BC，其中正确结论的个数是（）

A、3 B、2 C、1 D、0

查看试题解析
9. 在直角坐标系中，一直线a向下平移3个单位后所得直线b经过点A（0，3），将直线b绕点A顺时针旋转60°后所得直线经过点B（﹣ $\sqrt{3}$ ，0），则直线a的函数关系式为（）

A、y=﹣ $\sqrt{3}$ x B、y=﹣ $\frac{\sqrt{3}}{3}$ x C、y=﹣ $\sqrt{3}$ x+6 D、y=﹣ $\frac{\sqrt{3}}{3}$ x+6

查看试题解析
10. 已知△ABC的三条边长分别为3，4，6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（）

A、6条 B、7条 C、8条 D、9条

查看试题解析

二、填空题

11. 分解因式：x³﹣4x= ．

查看试题解析
12. 据国网江苏电力公司分析，我省预计今夏统调最高用电负荷将达到86000000千瓦，这个数据用科学记数法可表示为千瓦．

查看试题解析
13. 方程 $\frac{2}{x + 2} = \frac{1}{x}$ 的解是．

查看试题解析
14. 已知双曲线y= $\frac{k - 1}{x}$ 经过点（﹣2，1），则k的值等于．

查看试题解析
15. 如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于．

查看试题解析
16. 如图，▱ABCD中，AE⊥BD于E，∠EAC=30°，AE=3，则AC的长等于．

查看试题解析
17. 如图，已知点P是半径为1的⊙A上一点，延长AP到C，使PC=AP，以AC为对角线作▱ABCD．若AB= $\sqrt{3}$ ，则▱ABCD面积的最大值为．

查看试题解析
18. 如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最小值是．

查看试题解析

三、解答题

19.

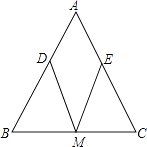
(1)、 ${(\sqrt{3})}^{2}$ ﹣|﹣2|+（﹣2）⁰；

(2)、（x+1）（x﹣1）﹣（x﹣2）² ．

查看试题解析
20.

(1)、解方程：x²﹣5x﹣6=0；

(2)、解不等式组： ${\begin{matrix} 2 (x - 1) \geq x + 1 \\ x - 2 > \frac{1}{3} (2 x - 1) \end{matrix}$ ．

查看试题解析
21. 如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．

查看试题解析
22. 如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．

(1)、若∠B=70°，求∠CAD的度数；

(2)、若AB=4，AC=3，求DE的长．

查看试题解析
23. 为了解“数学思想作为对学习数学帮助有多大？”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查，并将调查得到的数据用下面的扇形图和下表来表示（图、表都没制作完成）．
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息．

(1)、请问：这次共有多少名学生参与了问卷调查？

(2)、算出表中a、b的值．
（注：计算中涉及到的“人数”均精确到1）

查看试题解析
24. 三个小球分别标有﹣2，0，1三个数，这三个球除了标的数不同外，其余均相同，将小球放入一个不透明的布袋中搅匀．

(1)、从布袋中任意摸出一个小球，将小球上所标之数记下，然后将小球放回袋中，搅匀后再任意摸出一个小球，再记下小球上所标之数，求两次记下之数的和大于0的概率．（请用“画树状图”或“列表”等方法给出分析过程，并求出结果）

(2)、从布袋中任意摸出一个小球，将小球上所标之数记下，然后将小球放回袋中，搅匀后再任意摸出一个小球，将小球上所标之数再记下，…，这样一共摸了13次．若记下的13个数之和等于﹣4，平方和等于14．求：这13次摸球中，摸到球上所标之数是0的次数．

查看试题解析
25.

(1)、如图1，Rt△ABC中，∠B=90°，AB=2BC，现以C为圆心、CB长为半径画弧交边AC于D，再以A为圆心、AD为半径画弧交边AB于E．求证： $\frac{A E}{A B}$ = $\frac{\sqrt{5} - 1}{2}$ ．（这个比值 $\frac{\sqrt{5} - 1}{2}$ 叫做AE与AB的黄金比．）

(2)、如果一等腰三角形的底边与腰的比等于黄金比，那么这个等腰三角形就叫做黄金三角形．请你以图2中的线段AB为腰，用直尺和圆规，作一个黄金三角形ABC．
（注：直尺没有刻度！作图不要求写作法，但要求保留作图痕迹，并对作图中涉及到的点用字母进行标注）

查看试题解析
26.
如图，二次函数y=ax²+bx（a＜0）的图象过坐标原点O，与x轴的负半轴交于点A，过A点的直线与y轴交于B，与二次函数的图象交于另一点C，且C点的横坐标为﹣1，AC：BC=3：1．

(1)、求点A的坐标；

(2)、设二次函数图象的顶点为F，其对称轴与直线AB及x轴分别交于点D和点E，若△FCD与△AED相似，求此二次函数的关系式．

查看试题解析
27. 某发电厂共有6台发电机发电，每台的发电量为300万千瓦/月．该厂计划从今年7月开始到年底，对6台发电机各进行一次改造升级．每月改造升级1台，这台发电机当月停机，并于次月再投入发电，每台发电机改造升级后，每月的发电量将比原来提高20%．已知每台发电机改造升级的费用为20万元．将今年7月份作为第1个月开始往后算，该厂第x（x是正整数）个月的发电量设为y（万千瓦）．

(1)、求该厂第2个月的发电量及今年下半年的总发电量；

(2)、求y关于x的函数关系式；

(3)、如果每发1千瓦电可以盈利0.04元，那么从第1个月开始，至少要到第几个月，这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω₁（万元），将超过同样时间内发电机不作改造升级时的发电盈利总额ω₂（万元）？

查看试题解析
28.
如图1，已知点A（2，0），B（0，4），∠AOB的平分线交AB于C，一动点P从O点出发，以每秒2个单位长度的速度，沿y轴向点B作匀速运动，过点P且平行于AB的直线交x轴于Q，作P、Q关于直线OC的对称点M、N．设P运动的时间为t（0＜t＜2）秒．

(1)、求C点的坐标，并直接写出点M、N的坐标（用含t的代数式表示）；

(2)、
设△MNC与△OAB重叠部分的面积为S．
①试求S关于t的函数关系式；
②在图2的直角坐标系中，画出S关于t的函数图象，并回答：S是否有最大值？若有，写出S的最大值；若没有，请说明理由．

查看试题解析

选项	帮助很大	帮助较大	帮助不大	几乎没有帮助
人数	a	543	269	b