河北省石家庄市新华区2019年初中毕业生教学质量检测数学试卷
试卷更新日期:2019-05-08 类型:中考模拟
一、选择题(共42分)
-
1. 下列四个图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、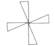 D、
D、 2. 在下列气温的变化中,能够反映温度上升5℃的是( )A、气温由-3C到2℃ B、气温由-1℃到-6℃ C、气温由-1℃到5℃ D、气温由4℃到-1℃3. 在下列各图形中,不是正方体的展开图的是( )A、
2. 在下列气温的变化中,能够反映温度上升5℃的是( )A、气温由-3C到2℃ B、气温由-1℃到-6℃ C、气温由-1℃到5℃ D、气温由4℃到-1℃3. 在下列各图形中,不是正方体的展开图的是( )A、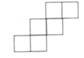 B、
B、 C、
C、 D、
D、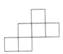 4. 近似数1.23×103精确到( )A、百分位 B、十分位 C、个位 D、十位5. 将一幅三角尺按图所示的方式摆放(两条直角边在同一条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为( )
4. 近似数1.23×103精确到( )A、百分位 B、十分位 C、个位 D、十位5. 将一幅三角尺按图所示的方式摆放(两条直角边在同一条直线上,且两锐角顶点重合),连接另外两条锐角顶点,并测得∠1=47°,则∠2的度数为( ) A、60° B、58° C、45° D、43°6. 如图,设一枚5角硬币的半径为1个单位长度,将这枚硬币放置在平面内一条数轴上,使硬币边缘上一点P与原点O重合,让这枚硬币沿数轴正方向无滑动滚动,转动一周时,点P到达数轴上点P'的位置,则点P'所对应的数为( )
A、60° B、58° C、45° D、43°6. 如图,设一枚5角硬币的半径为1个单位长度,将这枚硬币放置在平面内一条数轴上,使硬币边缘上一点P与原点O重合,让这枚硬币沿数轴正方向无滑动滚动,转动一周时,点P到达数轴上点P'的位置,则点P'所对应的数为( )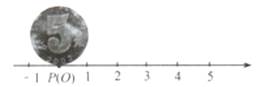 A、2π B、6.28 C、π D、3.147. 化简 的结果为( )A、x2 B、 C、 D、8. 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与从A村到B村的方向一致,则应顺时针转动的度数为( )
A、2π B、6.28 C、π D、3.147. 化简 的结果为( )A、x2 B、 C、 D、8. 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与从A村到B村的方向一致,则应顺时针转动的度数为( )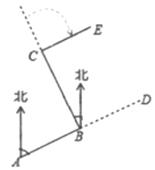 A、50° B、75° C、100° D、105°9. 某公司承担了制作600个道路交通指引标志的任务,原计划x天完成,实际平均每天多制作了10个,因此提前5天完成任务。根据题意,下列方程正确的是( )A、 B、 C、 D、10. 如图,将正五边形ABCDE沿逆时针方向绕其顶点A旋转,若使点B落在AE边所在的直线上,则旋转的角度可以是( )
A、50° B、75° C、100° D、105°9. 某公司承担了制作600个道路交通指引标志的任务,原计划x天完成,实际平均每天多制作了10个,因此提前5天完成任务。根据题意,下列方程正确的是( )A、 B、 C、 D、10. 如图,将正五边形ABCDE沿逆时针方向绕其顶点A旋转,若使点B落在AE边所在的直线上,则旋转的角度可以是( ) A、72° B、54° C、45° D、36°11. 将一元二次方程x2-6x+5=0配方后,原方程变形为( )A、(x-3)2=5 B、(x-6)2=5 C、(x-6)2=4 D、(x-3)2=412. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、13. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )
A、72° B、54° C、45° D、36°11. 将一元二次方程x2-6x+5=0配方后,原方程变形为( )A、(x-3)2=5 B、(x-6)2=5 C、(x-6)2=4 D、(x-3)2=412. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、13. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长度为( )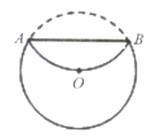 A、 B、2 C、2 D、(1+2 )14. 把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m可以取得的整数值有( )A、4个 B、5个 C、6个 D、7个15. 如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF。在:下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形。其中正确的是( )
A、 B、2 C、2 D、(1+2 )14. 把直线y=-x-3向上平移m个单位后,与直线y=2x+4的交点在第二象限,则m可以取得的整数值有( )A、4个 B、5个 C、6个 D、7个15. 如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF。在:下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形。其中正确的是( )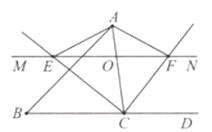 A、①④ B、①② C、①②③ D、②③④16. 如图,抛物线L:y=- (x-t)(x-t+4)(常数t>0),双曲线y= (x>0).设L与双曲线有个交点的横坐标为x0 , 且满足3<x0<4,在L位置随t变化的过程中,t的取值范围是( )
A、①④ B、①② C、①②③ D、②③④16. 如图,抛物线L:y=- (x-t)(x-t+4)(常数t>0),双曲线y= (x>0).设L与双曲线有个交点的横坐标为x0 , 且满足3<x0<4,在L位置随t变化的过程中,t的取值范围是( )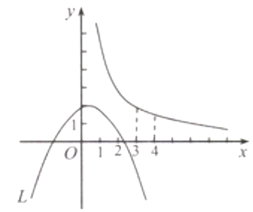 A、 <t<2 B、3<t<4 C、4<t<5 D、5<t<7
A、 <t<2 B、3<t<4 C、4<t<5 D、5<t<7二、填空题(共12分)
-
17. (-2)3= .18. 分解因式:ab2-4ab+4a=.19. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,以AC为斜边作Rt△ACC1 , 使∠CAC1=30°,Rt△ACC1的面积记为S1 , 则S1=;再以AC1为斜边作Rt△AC1C2 , 使∠C1AC2=30°,Rt△AC1C2的面积记为S2 , ……,以此类推,则Sn=(用含n的式子表示)
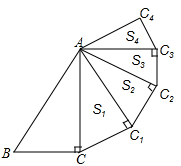
三、解答题(共66分)
-
20. 在多项式的乘法公式中,完全平方公式(a+b)2=a2+2ab+b2是其中重要的一个。(1)、请补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)
=a2+++b2
=a2++b2
(2)、如图,将边长为a+b的正方形分割成I、Ⅱ、Ⅲ、IV四部分,请你结合图给出完全平方公式的几何解释。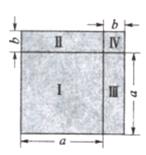 (3)、用完全平方公式求5982的值。21. 为在中小学生中普及交通法规常识,倡导安全出行,某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛.为了解市七年级学生的竞赛成绩,随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和频数分布直方图(频数分布直方图中有一处错误).
(3)、用完全平方公式求5982的值。21. 为在中小学生中普及交通法规常识,倡导安全出行,某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛.为了解市七年级学生的竞赛成绩,随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和频数分布直方图(频数分布直方图中有一处错误).组别(单位:分)
频数
频率
50.5~60.5
20
0.1
60.5~70.5
40
0.2
70.5~80.5
70
b
80.5~90.5
a
0.3
90.5~100.5
10
0.05

请根据图表信息回答下列问题:
(1)、在频数分布表中,a= , b=。(2)、指出频数分布直方图中的错误,并在图上改正;(3)、甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问:甲同学的成绩应在什么范围?(4)、全市共有5000名七年级学生,若规定成绩在80分以上(不含80分)为优秀,估计这次竞赛中成绩为优秀的学生有多少人?22. 【探究】(1)、观察下列算式,并完成填空:1=12
1+3=4=22:
1+3+5=9=32:
1+3+5+7=16=42:
1+3+5+…+(2n-1)= . (n是正整数)
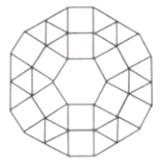
(2)、如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推。①第3层中分别含有 ▲ 块正方形和 ▲ 块正三角形地板砖:
②第n层中含有 ▲ 块正三角形地板砖(用含n的代数式表示)。
【应用】
该市打算在一个新建广场中央,采用图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
 23. 已知:如图,作∠AOB的平分线OP,在∠AOB的两边上分别截取OA=0B,再以点A为圆心,线段OA长为半径画弧,交OP于点P,连接BP.
23. 已知:如图,作∠AOB的平分线OP,在∠AOB的两边上分别截取OA=0B,再以点A为圆心,线段OA长为半径画弧,交OP于点P,连接BP.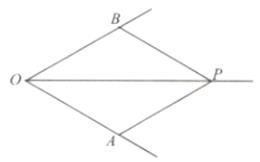 (1)、求证:四边形OAPB是菱形;(2)、尺规作图:作线段OA的垂直平分线EF,分别交OP于点E,OA于点F,连接BE(不写作法,保留作图痕迹):(3)、当∠AOB=60°时,判断△PBE的形状,并说明理由.24. 如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.
(1)、求证:四边形OAPB是菱形;(2)、尺规作图:作线段OA的垂直平分线EF,分别交OP于点E,OA于点F,连接BE(不写作法,保留作图痕迹):(3)、当∠AOB=60°时,判断△PBE的形状,并说明理由.24. 如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.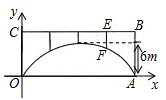 (1)、建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;(2)、求支柱EF的长度;(3)、拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米?25. 如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,点C是⊙O上任意一点,连接BC,OC.将OC绕点O按顺时针方向旋转90°,交⊙O于点D,连接AD.
(1)、建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;(2)、求支柱EF的长度;(3)、拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米?25. 如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,点C是⊙O上任意一点,连接BC,OC.将OC绕点O按顺时针方向旋转90°,交⊙O于点D,连接AD.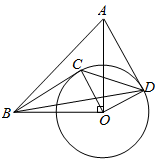 (1)、当AD与⊙O相切时,
(1)、当AD与⊙O相切时,①求证:BC是⊙O的切线;
②求点C到OB的距离。
(2)、连接BD,CD,当△BCD的面积最大时,点B到CD的距离为 .26. 如图,直线y=2x+2与x轴,y轴分别交于A,B两点,与反比例函数y= (x>0)的图象交于点M,过M作MH⊥x轴于点H,且AB=BM,点N(a,1)在反比例函数y= (x>0)的图象上。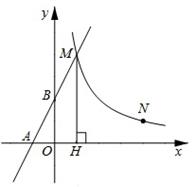 (1)、求k的值;(2)、在x轴的正半轴上存在一点P,使得PM+PN的值最小,求点P的坐标;(3)、点N关于x轴的对称点为N',把△ABO向右平移m个单位到△A'B'O'的位置,当N'A'+N'B'取得最小值时,请你在横线上直接写出m的值,m= .
(1)、求k的值;(2)、在x轴的正半轴上存在一点P,使得PM+PN的值最小,求点P的坐标;(3)、点N关于x轴的对称点为N',把△ABO向右平移m个单位到△A'B'O'的位置,当N'A'+N'B'取得最小值时,请你在横线上直接写出m的值,m= .