2014年江苏省泰州市中考数学试卷

试卷更新日期：2017-05-17 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2的相反数等于（）

A、﹣2 B、2 C、- $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、x³•x³=2x⁶ B、（﹣2x²）²=﹣4x⁴ C、（x³）²=x⁶ D、x⁵÷x=x⁵

查看试题解析
3. 一组数据﹣1、2、3、4的极差是（）

A、5 B、4 C、3 D、2

查看试题解析
4. 一个几何体的三视图如图所示，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
5. 下列图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）

A、1，2，3 B、1，1， $\sqrt{2}$ C、1，1， $\sqrt{3}$ D、1，2， $\sqrt{3}$

查看试题解析

二、填空题

7. $\sqrt{4}$ = ．

查看试题解析
8. 点P（﹣2，3）关于x轴的对称点P′的坐标为．

查看试题解析
9. 五边形的内角和为．

查看试题解析
10. 将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后，得到的图象对应的函数关系式为．

查看试题解析
11. 如图，直线a、b与直线c相交，且a∥b，∠α=55°，则∠β= ．

查看试题解析
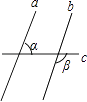12. 任意抛掷一枚均匀的骰子一次，朝上的点数大于4的概率等于．

查看试题解析
13. 圆锥的底面半径为6cm，母线长为10cm，则圆锥的侧面积为cm² ．

查看试题解析
14. 已知a²+3ab+b²=0（a≠0，b≠0），则代数式 $\frac{b}{a} + \frac{a}{b}$ 的值等于．

查看试题解析
15. 如图，A、B、C、D依次为一直线上4个点，BC=2，△BCE为等边三角形，⊙O过A、D、E3点，且∠AOD=120°．设AB=x，CD=y，则y与x的函数关系式为．

查看试题解析
16. 如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ=AE，则AP等于cm．

查看试题解析

三、解答题

17.

(1)、计算：﹣2⁴﹣ $\sqrt{12}$ +|1﹣4sin60°|+（π﹣ $\frac{2}{3}$ ）⁰；

(2)、解方程：2x²﹣4x﹣1=0．

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{3}{x + 2}$ ）÷ $\frac{x - 1}{x^{2} + 2 x}$ ﹣ $\frac{x}{x + 1}$ ，其中x满足x²﹣x﹣1=0．

查看试题解析
19. 某校为了解2013年八年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如下的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．
类别
科普类
教辅类
文艺类
其他
册数（本）
128
80
m
48

(1)、求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数；

(2)、该校2013年八年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？

查看试题解析
20. 某篮球运动员去年共参加40场比赛，其中3分球的命中率为0.25，平均每场有12次3分球未投中．

(1)、该运动员去年的比赛中共投中多少个3分球？

(2)、在其中的一场比赛中，该运动员3分球共出手20次，小亮说，该运动员这场比赛中一定投中了5个3分球，你认为小亮的说法正确吗？请说明理由．

查看试题解析
21. 今年“五一”小长假期间，某市外来与外出旅游的总人数为226万人，分别比去年同期增长30%和20%，去年同期外来旅游比外出旅游的人数多20万人．求该市今年外来和外出旅游的人数．

查看试题解析
22. 图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1.6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0.8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0.1m）．
（参考数据：sin12°=cos78°≈0.21，sin68°=cos22°≈0.93，tan68°≈2.48）

查看试题解析
23. 如图，BD是△ABC的角平分线，点E，F分别在BC、AB上，且DE∥AB，EF∥AC．

(1)、求证：BE=AF；

(2)、若∠ABC=60°，BD=6，求四边形ADEF的面积．

查看试题解析
24. 某研究所将某种材料加热到1000℃时停止加热，并立即将材料分为A、B两组，采用不同工艺做降温对比实验，设降温开始后经过x min时，A、B两组材料的温度分别为y_A℃、y_B℃，y_A、y_B与x的函数关系式分别为y_A=kx+b，y_B= $\frac{1}{4}$ （x﹣60）²+m（部分图象如图所示），当x=40时，两组材料的温度相同．

(1)、分别求y_A、y_B关于x的函数关系式；

(2)、当A组材料的温度降至120℃时，B组材料的温度是多少？

(3)、在0＜x＜40的什么时刻，两组材料温差最大？

查看试题解析
25. 如图，平面直角坐标系xOy中，一次函数y=﹣ $\frac{3}{4}$ x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．

(1)、若直线AB与 $\hat{C D}$ 有两个交点F、G．
①求∠CFE的度数；
②用含b的代数式表示FG² ，并直接写出b的取值范围；

(2)、设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．

查看试题解析
26.
平面直角坐标系xOy中，点A、B分别在函数y₁= $\frac{4}{x}$ （x＞0）与y₂=﹣ $\frac{4}{x}$ （x＜0）的图象上，A、B的横坐标分别为
a、b．

(1)、若AB∥x轴，求△OAB的面积；

(2)、若△OAB是以AB为底边的等腰三角形，且a+b≠0，求ab的值；

(3)、作边长为3的正方形ACDE，使AC∥x轴，点D在点A的左上方，那么，对大于或等于4的任意实数a，CD边与函数y₁= $\frac{4}{x}$ （x＞0）的图象都有交点，请说明理由．

查看试题解析

类别	科普类	教辅类	文艺类	其他
册数（本）	128	80	m	48