2011年江苏省淮安市中考数学试卷
试卷更新日期:2017-05-17 类型:中考真卷
一、选择题
-
1. 3的相反数是( )A、﹣3 B、﹣ C、 D、32. 下列交通标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 据第六次全国人口普查数据公报,淮安市常住人口约为480万人.480万(4800000)用科学记数法可表示为( )A、4.8×104 B、4.8×105 C、4.8×106 D、4.8×1074. 如图所示的几何体的主视图是( )
3. 据第六次全国人口普查数据公报,淮安市常住人口约为480万人.480万(4800000)用科学记数法可表示为( )A、4.8×104 B、4.8×105 C、4.8×106 D、4.8×1074. 如图所示的几何体的主视图是( ) A、
A、 B、
B、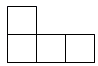 C、
C、 D、
D、 5. 在菱形ABCD中,AB=5cm,则此菱形的周长为( )A、5cm B、15cm C、20cm D、25cm6. 某地区连续5天的最高气温(单位:℃)分别是:30,33,24,29,24.这组数据的中位数是( )A、29 B、28 C、24 D、97. 不等式 的解集是( )A、x<﹣2 B、x<﹣1 C、x<0 D、x>28. 如图,反比例函数y= 的图象经过点A(﹣1,﹣2).则当x>1时,函数值y的取值范围是( )
5. 在菱形ABCD中,AB=5cm,则此菱形的周长为( )A、5cm B、15cm C、20cm D、25cm6. 某地区连续5天的最高气温(单位:℃)分别是:30,33,24,29,24.这组数据的中位数是( )A、29 B、28 C、24 D、97. 不等式 的解集是( )A、x<﹣2 B、x<﹣1 C、x<0 D、x>28. 如图,反比例函数y= 的图象经过点A(﹣1,﹣2).则当x>1时,函数值y的取值范围是( ) A、y>1 B、0<y<l C、y>2 D、0<y<2
A、y>1 B、0<y<l C、y>2 D、0<y<2二、填空题
-
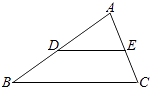
9. 计算:a4•a2= .10. 如图,在△ABC中,D、E分别是边AB、AC的中点,BC=8,则DE= .
 11. 分解因式:ax+ay= .12. 如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2= .
11. 分解因式:ax+ay= .12. 如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2= . 13. 一元二次方程x2﹣4=0的解x= .
13. 一元二次方程x2﹣4=0的解x= .
14. 抛物线y=x2﹣2x+3的顶点坐标是 .15. 在半径为6cm的圆中,60°的圆心角所对的弧长等于 cm(结果保留π).16. 有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为 .17. 在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 . (写出一种即可)18. 如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2 ,则△ABC的周长等于 .
三、解答题
-
19.(1)、计算: ;(2)、化简:(a+b)2+b(a﹣b).20. 如图,四边形ABCD是平行四边形,E、F分别是BC.AD上的点,∠1=∠2
求证:△ABE≌△CDF.
 21. 如图,有牌面数字都是2,3,4的两组牌.从毎组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率.
21. 如图,有牌面数字都是2,3,4的两组牌.从毎组牌中各随机摸出一张,请用画树状图或列表的方法,求摸出的两张牌的牌面数字之和为6的概率. 22. 七(1)班的大课间活动丰富多彩,小峰与小月进行跳绳比赛.在相同的时间内,小峰跳了100个,小月跳了140个.如果小月比小峰毎分钟多跳20个,试求出小峰毎分钟跳绳多少个?23. 图1为平地上一幢建筑物与铁塔图,图2为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度.
22. 七(1)班的大课间活动丰富多彩,小峰与小月进行跳绳比赛.在相同的时间内,小峰跳了100个,小月跳了140个.如果小月比小峰毎分钟多跳20个,试求出小峰毎分钟跳绳多少个?23. 图1为平地上一幢建筑物与铁塔图,图2为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度. 24. 阳光中学九(1)班同学在一次综合实践活动中,对本县居民参加“全民医保“情况进行了调查.同学们利用节假日随机调查了2000人,对调查结果进行了系统分析.绘制出两幅不完整的统计图:
24. 阳光中学九(1)班同学在一次综合实践活动中,对本县居民参加“全民医保“情况进行了调查.同学们利用节假日随机调查了2000人,对调查结果进行了系统分析.绘制出两幅不完整的统计图:
(注:图中A表示“城镇职工基本医疗保险”,B表示“城镇居民基本医疗保险”;C表示“新型农村合作医疗”;D表示其他情况)
(1)、补全条形统计图;(2)、在本次调查中,B类人数占被调查人数的百分比为(3)、据了解,国家对B类人员每人每年补助155元,已知该县人口约80万人,请估计该县B类人员每年享受国家补助共多少万元?25. 如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.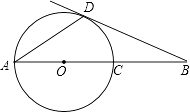 (1)、直线BD是否与⊙O相切?为什么?(2)、连接CD,若CD=5,求AB的长.26. 如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)、直线BD是否与⊙O相切?为什么?(2)、连接CD,若CD=5,求AB的长.26. 如图.已知二次函数y=﹣x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B. (1)、求此二次函数关系式和点B的坐标;(2)、在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.27. 小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式:
(1)、求此二次函数关系式和点B的坐标;(2)、在x轴的正半轴上是否存在点P.使得△PAB是以AB为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.27. 小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1 , 时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式:请你完成:
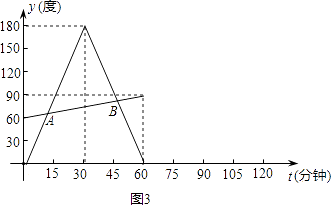
 (1)、求出图3中y2与t的函数关系式;(2)、直接写出A、B两点的坐标,并解释这两点的实际意义;(3)、若小华继续观察一个小时,请你在题图3中补全图象.28. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)、求出图3中y2与t的函数关系式;(2)、直接写出A、B两点的坐标,并解释这两点的实际意义;(3)、若小华继续观察一个小时,请你在题图3中补全图象.28. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)、当t=1时,正方形EFGH的边长是 . 当t=3时,正方形EFGH的边长是 .(2)、当0<t≤2时,求S与t的函数关系式;(3)、直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?