上海市金山区2019届高三下学期数学二模质量监控试卷

试卷更新日期：2019-05-06 类型：高考模拟

进入出卷网下载

一、单选题

1. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，下列计算结果一定不等于0的是（）

A、 $\overset{⇀}{A D_{1}} \cdot \overset{⇀}{B_{1} C}$ B、 $\overset{⇀}{B D_{1}} \cdot \overset{⇀}{A C}$ C、 $\overset{⇀}{D C} \cdot \overset{⇀}{A D_{1}}$ D、 $\overset{⇀}{B D_{1}} \cdot \overset{⇀}{B_{1} C_{1}}$

查看试题解析
2. 在我国南北朝时期，数学家祖暅在实践的基础上提出了体积计算的原理：“幂势既同，则积不容异”．其意思是，用一组平行平面截两个几何体，若在任意等高处的截面面积都对应相等，则两个几何体的体积必然相等．根据祖暅原理，“两几何体A、B的体积不相等”是“A、B在等高处的截面面积不恒相等”的（）条件

A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要

查看试题解析
3. 设 $F_{1}$ 、 $F_{2}$ 是双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ $(a > 0, b > 0)$ 的两个焦点， $P$ 是 $C$ 上一点，若 $| P F_{1} | + | P F_{2} | = 6 a$ ， $∠ P F_{1} F_{2}$ 是△ $P F_{1} F_{2}$ 的最小内角，且 $∠ P F_{1} F_{2} = 30^{°}$ ，则双曲线 $C$ 的渐近线方程是（）

A、 $x \pm \sqrt{2} y = 0$ B、 $\sqrt{2} x \pm y = 0$ C、 $x \pm 2 y = 0$ D、 $2 x \pm y = 0$

查看试题解析
4. 若实数 $a$ 、 $b$ 满足 ${\begin{matrix} a + b - 2 \geq 0 \\ b - a - 1 \leq 0 \\ a \leq 1 \end{matrix}$ ，则 $\frac{b^{2} - 3 a b}{a^{2}}$ 的取值范围是（）

A、 $[- 2 ， 0]$ B、 $[- \frac{9}{4} ， + \infty)$ C、 $[- \frac{9}{4} ， - 2]$ D、 $[- \frac{9}{4} ， 0]$

查看试题解析

二、填空题

5. 函数 $f (x) = \sqrt{x - 4}$ 的定义域是

查看试题解析
6. 函数 $y = {(sin x + cos x)}^{2}$ 的最小正周期是

查看试题解析
7. 若关于 $x$ 、 $y$ 的线性方程组的增广矩阵为 $(\begin{matrix} m & 0 \\ 0 & 3 \end{matrix} \begin{matrix} 6 \\ n \end{matrix})$ ，该方程组的解为 ${\begin{matrix} x = - 3 \\ y = 4 \end{matrix}$ ，则 $m + n$ 的值是

查看试题解析
8. 二项式 ${(x+1)}^{7}$ 的展开式中含 $x^{3}$ 项的系数值是

查看试题解析
9. 已知全集U = R，集合 $P = {y | y = \frac{1}{x}, 0 < x < 1}$ ，则 $∁_{U} P =$

查看试题解析
10. 若 $z_{1} = 1 + i$ ， $z_{2} = a - i$ ，其中i为虚数单位，且 $z_{1} \cdot \bar{z_{2}} \in$ R，则 $| z_{2} |_{} =$

查看试题解析
11. 方程 ${\begin{matrix} x = t + 1 \\ y = 3 - t^{2} \end{matrix}$ （t为参数，t∈R）所对应曲线的普通方程为

查看试题解析
12. 在Rt△ABC中， $∠ C = 90^{°}$ ， $A C = 4$ ，则 $\overset{⇀}{A B} \cdot \overset{⇀}{A C} =$

查看试题解析
13. 若生产某种零件需要经过两道工序，在第一、二道工序中生产出废品的概率分别为0.01、0.02，每道工序生产废品相互独立，则经过两道工序后得到的零件不是废品的概率是（结果用小数表示）

查看试题解析
14. 已知函数 $f (x) = sin x$ 和 $g (x) = \sqrt{π^{2} - x^{2}}$ 的定义域都是 $[- π, π]$ ，则它们的图像围成的区域面积是

查看试题解析
15. 若集合 $A = {x | x^{2} - (a + 2) x + 2 - a < 0 ，$ $x \in$ Z $}$ 中有且只有一个元素，则正实数 $a$ 的取值范围是

查看试题解析
16. 正方形ABCD的边长为2，对角线AC、BD相交于点O，动点P满足 $| \overset{⇀}{O P} |_{} = \frac{\sqrt{2}}{2}$ ，若 $\overset{⇀}{A P} = m \overset{⇀}{A B} + n \overset{⇀}{A D}$ ，其中m、n∈R，则 $\frac{2 m + 1}{2 n + 2}$ 的最大值是

查看试题解析

三、解答题

17. 已知△ $A B C$ 中， $tan A = \frac{1}{4}$ ， $tan B = \frac{3}{5}$ ， $A B = \sqrt{17}$ . 求：

(1)、角 $C$ 的大小；

(2)、△ABC中最小边的边长.

查看试题解析
18. 如图，已知点P在圆柱 $O O_{1}$ 的底面圆O上，AB为圆O的直径，圆柱 $O O_{1}$ 的侧面积为 $16 π$ ， $O A = 2$ ， $∠ A O P = 120^{°}$ .

(1)、求三棱锥 $A_{1} - A P B$ 的体积；

(2)、求直线 $A_{1} P$ 与底面 $P A B$ 所成角的大小.

查看试题解析
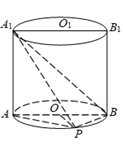19. 从金山区走出去的陈驰博士，在《自然—可持续性》杂志上发表的论文中指出：地球正在变绿，中国通过植树造林和提高农业效率，在其中起到了主导地位．已知某种树木的高度 $f (t)$ (单位：米)与生长年限 $t$ （单位：年，t∈N^*）满足如下的逻辑斯蒂函数： $f (t) = \frac{6}{1 + e^{- 0.5 t + 2}}$ ，其中e为自然对数的底数. 设该树栽下的时刻为0. $(ln 5 \approx 1.61)$

(1)、需要经过多少年，该树的高度才能超过5米？（精确到个位）

(2)、在第几年内，该树长高最快？

查看试题解析
20. 已知椭圆 $Γ$ ： $\frac{x^{2}}{m + 1} + \frac{y^{2}}{m} = 1$ ，过点 $D (- 1, 0)$ 的直线 $l$ ： $y = k (x + 1)$ 与椭圆 $Γ$ 交于M、N两点（M点在N点的上方），与 $y$ 轴交于点E.

(1)、当 $m = 1$ 且 $k = 1$ 时，求点M、N的坐标；

(2)、当 $m = 2$ 时，设 $\overset{⇀}{E M} = λ \overset{⇀}{D M}$ ， $\overset{⇀}{E N} = μ \overset{⇀}{D N}$ ，求证： $λ + μ$ 为定值，并求出该值；

(3)、当 $m = 3$ 时，点D和点F关于坐标原点对称，若△MNF的内切圆面积等于 $\frac{18}{49} π$ ，求直线 $l$ 的方程.

查看试题解析
21. 若数列 ${a_{n}}$ 、 ${b_{n}}$ 满足 $| a_{n + 1} - a_{n} | = b_{n}$ ( $n \in$ N*)，则称 ${b_{n}}$ 为数列 ${a_{n}}$ 的“偏差数列”.

(1)、若 ${b_{n}}$ 为常数列，且为 ${a_{n}}$ 的“偏差数列”，试判断 ${a_{n}}$ 是否一定为等差数列，并说明理由；

(2)、若无穷数列 ${a_{n}}$ 是各项均为正整数的等比数列，且 $a_{3} - a_{2} = 6$ ， ${b_{n}}$ 为数列 ${a_{n}}$ 的“偏差数列”，求 $lim_{n \to \infty} (\frac{1}{b_{1}} + \frac{1}{b_{2}} + \frac{1}{b_{3}} + \dots + \frac{1}{b_{n}})$ 的值；

(3)、设 $b_{n} = 6 - {(\frac{1}{2})}^{n + 1}$ ， ${b_{n}}$ 为数列 ${a_{n}}$ 的“偏差数列”， $a_{1} = 1$ ， $a_{2 n} \leq a_{2 n - 1}$ 且 $a_{2 n} \leq a_{2 n + 1}$ ，若 $| a_{n} |_{} \leq M$ 对任意 $n \in N^{*}$ 恒成立，求实数M的最小值.

查看试题解析