2019年广东省深圳市中考数学模拟预测卷1
试卷更新日期:2019-05-06 类型:中考模拟
一、选择题
-
1. ﹣5的相反数是( )A、﹣5 B、5 C、±5 D、2. 习近平主席在2018年新年贺词中指出,“安得广厦千万间,大庇天下寒土俱欢颜!”2017年,340万贫困人口实现易地扶贫搬迁,有了温暖的新家,各类棚户区改造开工提前完成600万套目标任务.将340万用科学记数法表示为( )A、0.34×107 B、34×105 C、3.4×105 D、3.4×1063. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列图形中是轴对称图形但不是中心对称图形的是( )A、
4. 下列图形中是轴对称图形但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列说法中,正确的是( )A、—个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小6. 下列计算中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )
5. 下列说法中,正确的是( )A、—个游戏中奖的概率是 ,则做10次这样的游戏一定会中奖 B、为了了解一批炮弹的杀伤半径,应采用全面调查的方式 C、一组数据8,8,7,10,6,8,9的众数是8 D、若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小6. 下列计算中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )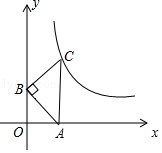 A、4 B、2 C、2 D、8. 如图,直线a∥b,直线 分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是( )
A、4 B、2 C、2 D、8. 如图,直线a∥b,直线 分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是( ) A、50° B、70° C、80° D、110°9. 宾馆有50间房供游客居住,当毎间房毎天定价为180元时,宾馆会住满;当毎间房毎天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房毎天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )A、(180+x﹣20)(50﹣ )=10890 B、(x﹣20)(50﹣ )=10890 C、x(50﹣ )﹣50×20=10890 D、(x+180)(50﹣ )﹣50×20=1089010. 如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )
A、50° B、70° C、80° D、110°9. 宾馆有50间房供游客居住,当毎间房毎天定价为180元时,宾馆会住满;当毎间房毎天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房毎天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )A、(180+x﹣20)(50﹣ )=10890 B、(x﹣20)(50﹣ )=10890 C、x(50﹣ )﹣50×20=10890 D、(x+180)(50﹣ )﹣50×20=1089010. 如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( )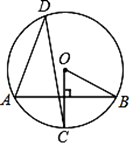 A、64° B、58° C、32° D、26°11. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2 , 且x1<x2 , 则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有( )
A、64° B、58° C、32° D、26°11. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,顶点坐标为(﹣2,﹣9a),下列结论:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有两个根x1和x2 , 且x1<x2 , 则﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四个根,则这四个根的和为﹣4.其中正确的结论有( )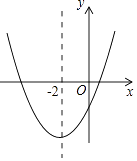 A、1个 B、2个 C、3个 D、4个12. 如图,在平面直角坐标系中,直线l1:y=﹣ x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A、1个 B、2个 C、3个 D、4个12. 如图,在平面直角坐标系中,直线l1:y=﹣ x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )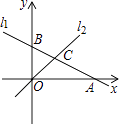 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
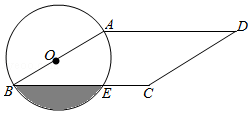
13. 分解因式:x3y﹣xy3= .14. 在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为15. 如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O交BC于点E,则阴影部分的面积为 .
 16. 如图,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF= .
16. 如图,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF= .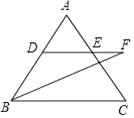
三、解答题
-
17. 计算: ﹣(1﹣ )0+sin45°+( )﹣118. 先化简再求值( ﹣y)÷ ﹣(x﹣2y)(x+y),其中x=﹣1,y=2.
19. “校园安全”受到全社会的广泛关注.某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请根据统计图中所提供的信息解答下列问题:

 (1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解” 程度的总人数.20. 如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.
(1)、接受问卷调查的学生共有人,扇形统计图中“了解”部分所对应扇形的圆心角为度;(2)、请补全条形统计图;(3)、若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解” 程度的总人数.20. 如图,已知∠AOB,OA=OB,点E在OB 上,四边形AEBF是矩形.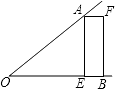 (1)、请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹);(2)、若∠AOB=45°,OA=OB=2 ,求BE的长.21. 我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际 每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货.求每月实际生产智能手机多少万部.22. 如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)、请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹);(2)、若∠AOB=45°,OA=OB=2 ,求BE的长.21. 我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际 每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货.求每月实际生产智能手机多少万部.22. 如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.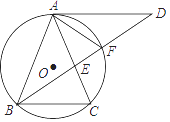 (1)、求∠DAF的度数;
(1)、求∠DAF的度数;
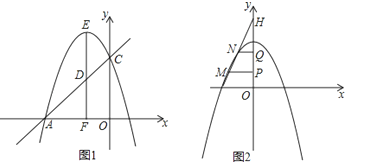
(2)、求证:AE2=EF•ED;(3)、求证:AD是⊙O的切线.23. 已知抛物线的C1顶点为E(﹣1,4),与y轴交于C(0,3).(1)求抛物线C1的解析式;
(2)如图1,过顶点E作EF⊥x轴于F点,交直线AC于D,点P、Q分别在抛物线C1和x轴上,若Q为(t,0),且以E、D、P、Q为顶点的四边形为平行四边形,求t的值;
(3)如图2,将抛物线C1向右平移一个单位得到抛物线C2 , 直线y=kx+6与y轴交于点H,与抛物线C2交于M、N两个不同点,分别过M、N两点作y轴的垂线,垂足分别为P、Q,当k的值在取值范围内发生变化时,式子+的值是否发生变化?若不变,请求其值.(解此题时不用相似知识)