安徽省合肥市包河区2018-2019学年九年级下学期数学第一次模拟考试试卷
试卷更新日期:2019-05-05 类型:中考模拟
一、选择题。(满分40分)
-
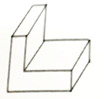
1. 以下4个数:0,-0.1,-1,-2,最小的是( )A、0 B、-0.1 C、-1 D、-22. 下列式子中,计算结果是a8的是( )A、a2+a6 B、a10-a2 C、a2·a6 D、(a2)33. 2018年移动支付调查报告发布城据:当前我国手机支付用户数量己达5.7亿,共中5.7亿用科学记数法表示为( )A、5.7×104 B、5.7×108 C、0.57×109 D、5.7×1074. 将一个机器零件按如图方式摆放,则它的左视图为( )
 A、
A、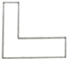 B、
B、 C、
C、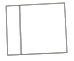 D、
D、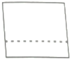 5. 如图,OF是∠BDC的平分线,AB∥CD,∠ABD=118°,则∠1的度数为( )
5. 如图,OF是∠BDC的平分线,AB∥CD,∠ABD=118°,则∠1的度数为( ) A、31° B、26° C、36° D、40°6. 某旅游景区去年第二季度游客数量比第一季度下降20%,第三、四季度游客数量持续增长,第四季度游客数量比第一季度增长15.2%,设第三、四季度的平均增长率为x,下列方程正确的是( )A、(1-20%)(1+x)2=1+15.2% B、(1-20%)(1+2x)=1+15.2% C、1+2x=(1-20%)(1+15.2%) D、(1+x)2=20%+15.2%7. 如图,若反比例函数y= (x<0)的图象经过点(- ,4),点A为图象上任意一点,点B在x轴负半轴上,连接AO,AB,当AB=OA时,△AOB的面积为( )
A、31° B、26° C、36° D、40°6. 某旅游景区去年第二季度游客数量比第一季度下降20%,第三、四季度游客数量持续增长,第四季度游客数量比第一季度增长15.2%,设第三、四季度的平均增长率为x,下列方程正确的是( )A、(1-20%)(1+x)2=1+15.2% B、(1-20%)(1+2x)=1+15.2% C、1+2x=(1-20%)(1+15.2%) D、(1+x)2=20%+15.2%7. 如图,若反比例函数y= (x<0)的图象经过点(- ,4),点A为图象上任意一点,点B在x轴负半轴上,连接AO,AB,当AB=OA时,△AOB的面积为( ) A、1 B、2 C、4 D、无法确定8. 为了落实“垃圾分类”,环卫部门将某住宅小区的垃圾箱设置为A,B,C三类,广宇家附近恰好有A,B,C三类垃圾箱各一个,广宇姐姐将家中的垃圾地应分成A,B两包,如果广宇将两包垃圾随机投放到其中的两个垃圾箱中,能实现对应投放的概率是( )A、 B、 C、 D、9. 如图,在四边后ABCD中,∠A=∠B=90°,∠C=60°,BC=CD=8,将四边形ABCD折叠,使点C与点A重合,折痕为EF,则BE的长为( )
A、1 B、2 C、4 D、无法确定8. 为了落实“垃圾分类”,环卫部门将某住宅小区的垃圾箱设置为A,B,C三类,广宇家附近恰好有A,B,C三类垃圾箱各一个,广宇姐姐将家中的垃圾地应分成A,B两包,如果广宇将两包垃圾随机投放到其中的两个垃圾箱中,能实现对应投放的概率是( )A、 B、 C、 D、9. 如图,在四边后ABCD中,∠A=∠B=90°,∠C=60°,BC=CD=8,将四边形ABCD折叠,使点C与点A重合,折痕为EF,则BE的长为( ) A、1 B、2 C、 D、10. 已知,△ABC中,∠BAC=135°,AB=AC=2 ,P为边AC上一动点,PQ∥BC交AB于Q,设PC=x, △PCQ的面积为y,则y与x的函数关系图象是( )A、
A、1 B、2 C、 D、10. 已知,△ABC中,∠BAC=135°,AB=AC=2 ,P为边AC上一动点,PQ∥BC交AB于Q,设PC=x, △PCQ的面积为y,则y与x的函数关系图象是( )A、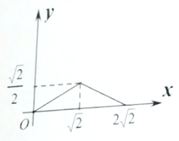 B、
B、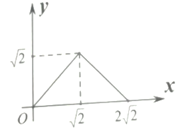 C、
C、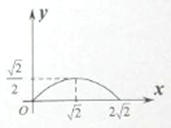 D、
D、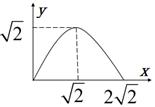
二、填空题(满分20分)
-
11. 64的立方根是 。12. 在函效y= 中,自变量x的取值范围是。13. 如图,OC是⊙O的半径,弦AB⊥OC于点D,点E在⊙O上,EB恰好经过圆心O,连接EC。若∠B=∠E,OD= ,则劣弧AB的长为。
 14. 如图,在矩形ABCD中,AD=4,AC=8,点E是AB的中点,点F是对角线AC上一点,△GEF与△AEF关于直线EF对称,EG交AC于点H,当△CGH中有一个内角为90°时,则CG的长为。
14. 如图,在矩形ABCD中,AD=4,AC=8,点E是AB的中点,点F是对角线AC上一点,△GEF与△AEF关于直线EF对称,EG交AC于点H,当△CGH中有一个内角为90°时,则CG的长为。
三、(满分16分)
-
15. 解不等式: >x-316. 计算:
四、(满分16分)
-
17. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC。
 (1)、将△ABC绕格点O顺时针旋转90°,得到A'B'C',画出△A'B'C':(2)、尺规作图,过格点C作AB的垂线,标出垂足D(保留作图痕迹,不写作法)。(3)、线段CD的长为。18. 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年的著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题:
(1)、将△ABC绕格点O顺时针旋转90°,得到A'B'C',画出△A'B'C':(2)、尺规作图,过格点C作AB的垂线,标出垂足D(保留作图痕迹,不写作法)。(3)、线段CD的长为。18. 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年的著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: (1)、图中给出了七行数字,根据构成规律,第9行中从左边数第4个数是;(2)、第n行中从左边数第2个数为;第n行所有数字之和为。
(1)、图中给出了七行数字,根据构成规律,第9行中从左边数第4个数是;(2)、第n行中从左边数第2个数为;第n行所有数字之和为。五、(满分20分)
-
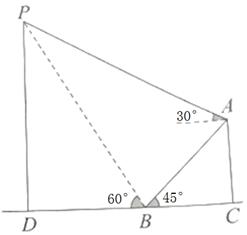
19. 如图,小明和小亮同时在山顶A和山脚B测得空中不明飞行物P的仰角分别为30°、60°.已知山的坡角∠ABC=45°,山的高度AC=1km,求不明飞行物P距地面BC的高PD(结果保留根号)。
 20. 如图,AB是⊙O的直径,点C在⊙O上,EO⊥AB,垂足为O,EO交AC于E,过点C作⊙O的切线CD交AB的延长线于点D.
20. 如图,AB是⊙O的直径,点C在⊙O上,EO⊥AB,垂足为O,EO交AC于E,过点C作⊙O的切线CD交AB的延长线于点D. (1)、求证:∠AEO+∠BCD=90°;(2)、若AC=CD=3,求⊙O的半径。
(1)、求证:∠AEO+∠BCD=90°;(2)、若AC=CD=3,求⊙O的半径。六、(本题满分12分)
-
21. 某校对九年级学生课外阅读情况进行了随机抽样调查,将调查的情况分为A,B,C,D四个等级,并制作了如下统计图(部分信息未给出)


请根据统计图中的信息解答下列问恩:
(1)、这次随机抽样调查的样本容量是;扇形统计图中x= ,y=(2)、补全条形统计图:(3)、已知该校九年级学生中课外阅读为A等级的共有60人,请估计九年级中其他等级各有多少人?七、(本题满分12分)
-
22. 如图,抛物线y=ax2+bx+3经过点A(-1,0)、B(4,0).E是线段OB的上一动点(点E不与O、B重合),过点E作x轴的垂线交抛物线于点D,交线段BC于点G.过点D作DF⊥BC,垂足为点F。
 (1)、求该抛物线的解析式:(2)、试求线段DF的长h的关于点E的横坐标x的函数解析式,并求出h的最大值。
(1)、求该抛物线的解析式:(2)、试求线段DF的长h的关于点E的横坐标x的函数解析式,并求出h的最大值。八、(本题满分14分)
-
23. 已如:△ABC中,BC=a,AC=b,AB=c,∠ACB=2∠B,CD是∠ACB的角平分线。
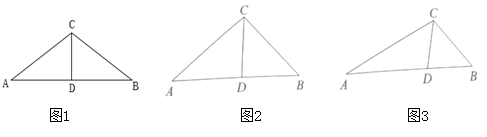 (1)、如图1,若∠A=∠B,则a、b、c三者之间满足的关系是(2)、如图2,求证:c2-b2=ab;(3)、如图3,若∠B=2∠A,求证:
(1)、如图1,若∠A=∠B,则a、b、c三者之间满足的关系是(2)、如图2,求证:c2-b2=ab;(3)、如图3,若∠B=2∠A,求证:
-
-