广东省茂名市高州市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-05-05 类型：期末考试

进入出卷网下载

一、选择题（共30分）

1. 下列几组数中不能作为直角三角形三边长度的是（）

A、 $a = 7 ， b = 24 ， c = 25$ B、 $a = 1.5 ， b = 2 ， c = 2.5$ C、 $a = \frac{2}{3} ， b = 2 ， c = \frac{5}{4}$ D、 $a = 15 ， b = 8 ， c = 17$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{20}$ =2 $\sqrt{10}$ B、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{6}$ C、 $\sqrt{4}$ ﹣ $\sqrt{2}$ = $\sqrt{2}$ D、 $\sqrt{{(- 3)}^{2}}$ =﹣3

查看试题解析
3. 坐标平面内下列各点中，在坐标轴上的是（）

A、（3，3） B、（﹣3，0） C、（﹣1，2） D、（﹣2，﹣3）

查看试题解析
4. 若函数y=（m﹣1）x^|^m^|﹣5是一次函数，则m的值为（）

A、±1 B、﹣1 C、1 D、2

查看试题解析
5. 一次函数y＝kx+3的图象如图所示，当y＜0时，x的取值范围是（）

A、x＜0 B、x＞0 C、x＜2 D、x＞2

查看试题解析
6. 下列方程组中，是二元一次方程组的是（）

A、 ${\begin{cases} x + \frac{1}{3} = 1 \\ y = x^{2} \end{cases}$ B、 ${\begin{cases} 3 x - y = 5 \\ 2 y - z = 6 \end{cases}$ C、 ${\begin{cases} \frac{x}{5} + \frac{y}{2} = 1 \\ x y = 1 \end{cases}$ D、 ${\begin{cases} \frac{x}{2} = 3 \\ y - 2 x = 4 \end{cases}$

查看试题解析
7. 下列方程组中，解是 ${\begin{matrix} x = - 5 \\ y = 1 \end{matrix}$ 的是（）

A、 ${\begin{matrix} x + y = 6 \\ x - y = 4 \end{matrix}$ B、 ${\begin{matrix} x + y = 6 \\ x - y = - 6 \end{matrix}$ C、 ${\begin{matrix} x + y = - 4 \\ x - y = - 6 \end{matrix}$ D、 ${\begin{matrix} x + y = - 4 \\ x - y = - 4 \end{matrix}$

查看试题解析
8. 一组数据3、5、8、3、4的众数与中位数分别是（　　）

A、3，8 B、3，3 C、3，4 D、4，3

查看试题解析
9. 如图所示是一条街道的路线图，若AB∥CD，且∠ABC＝130°，那么当∠CDE等于（）时，BC∥DE．

A、40° B、50° C、70° D、130°

查看试题解析
10. 如图，在Rt△ABC中，∠ACB＝90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A＝26°，则∠CDE度数为（）

A、71° B、64° C、80° D、45°

查看试题解析

二、填空题（共24分）

11. 等腰三角形的腰长为10，底边上的高为6，则底边长为．

查看试题解析
12. $\sqrt{2}$ ﹣1的相反数是，绝对值是．

查看试题解析
13. 在一次函数y＝2x+3中，y随x的增大而（填“增大”或“减小”），当0≤x≤5时，y的最小值为．

查看试题解析
14. 在三元一次方程x+y+2z＝5中，若x＝﹣1，y＝2，则z＝．

查看试题解析
15. 已知 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 是方程2x﹣ay＝3的一个解，那么a的值是．

查看试题解析
16. 如图，在△ABC中，BE平分∠ABC，CE平分∠ACB，∠A＝64°，则∠BEC＝度．

查看试题解析

三、解答题：

17. 解方程组和计算

(1)、 ${\begin{matrix} 2 x + y = 3 ① \\ 3 x - 5 y = 11 ② \end{matrix}$ （用代入法）

(2)、计算： $\frac{2 \sqrt{12} + \sqrt{3}}{\sqrt{3}}$ +（1﹣ $\sqrt{3}$ ）⁰

查看试题解析
18. 如图，已知一次函数y＝kx+b的图象经过A（﹣2，﹣1），B（1，3）两点，并且交x轴于点C，交y轴于点D．

(1)、求该一次函数的解析式；

(2)、求△AOB的面积．

查看试题解析
19. 某县为了了解2013年初中毕业生毕业后的去向，对部分初三学生进行了抽样调查，就初三学生的四种去向（A．读普通高中； B．读职业高中 C．直接进入社会就业； D．其它）进行数据统计，并绘制了两幅不完整的统计图（a）、（b）．
请问：

(1)、该县共调查了名初中毕业生；

(2)、将两幅统计图中不完整的部分补充完整；

(3)、若该县2013年初三毕业生共有4500人，请估计该县今年的初三毕业生中读普通高中的学生人数．

查看试题解析
20. 根据图中所给出的信息，求出每个篮球和每个羽毛球的价格．

查看试题解析
21. 某风景区集体门票的收费标准是：20人以内（含20人），每人25元；超过20人，超过部分每人10元．

(1)、写出应收门票费y（元）与游览人数x（人）之间的函数关系式；

(2)、利用（1）中的函数关系式计算，某班54人去该风景区旅游时，为购门票共花了多少元．

查看试题解析
22. 如图，在正方形ABCD中，AB＝4，AE＝2，DF＝1，请你判定△BEF的形状，并说明理由．

查看试题解析
23. 如图，在△ABC中，∠ACB＝90°，CE⊥AB于点E，AD＝AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，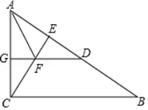

求证：

(1)、DF∥BC；

(2)、FG＝FE．

查看试题解析

24. 某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：

运输工具	运输费单价（元/吨•千米）	冷藏费单价（元/吨•小时）	过桥费（元）	装卸及管理费（元）
汽车	2	5	200	0
火车	1.8	5	0	1600

注：“元/吨•千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．

(1)、设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y₁（元）和y₂（元），试求出y₁和y₂和与x的函数关系式；

(2)、若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？

查看试题解析

25. 如图，直线OC、BC的函数关系式分别是y₁＝x和y₂＝﹣2x+6，直线BC与x轴交于点B，直线BA与直线OC相交于点A．

(1)、当x取何值时y₁＞y₂？

(2)、当直线BA平分△BOC的面积时，求点A的坐标．

查看试题解析