广东省江门市蓬江区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-05-05 类型：期末考试
一、选择题（共30分）
-
1. 下列标志是轴对称图形的是（ ）A、
B、
C、
D、
2. 某细胞的直径约为0.0000008米，该直径用科学记数法表示为（ ）A、0.8×10﹣5米 B、80×10﹣7米 C、8×10﹣6米 D、8×10﹣7米3. 正五边形的内角和是（ ）A、180° B、360° C、540° D、720°4. 使分式 有意义的x的取值范围是（ ）A、x≠1 B、x≠2 C、x≠ D、x≠05. 计算（﹣2b）3的结果是（ ）A、﹣8b3 B、8b3 C、﹣6b3 D、6b36. 如图，若△ABE≌△ACF，且AB＝5，AE＝2，则EC的长为（ ）
A、2 B、3 C、4 D、57. 如图，在△ABC中，AB＝AC，D为BC中点，∠BAD＝35°，则∠C的度数为（ ）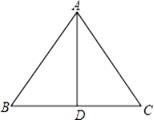
A、35° B、45° C、55° D、60°8. 下列各式中，是最简分式的是（ ）A、 B、 C、 D、9. 若三角形的三边长分别为3，1+2x，8，则x的取值范围是（ ）A、2＜x＜5 B、3＜x＜8 C、4＜x＜7 D、5＜x＜910. 若 ﹣ ＝4，则分式 的值是（ ）A、 B、 C、 D、2二、填空题（共24分）
-
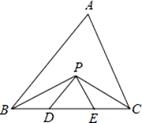
11. 在△ABC中，若∠A＝90°，∠B＝50°，则∠C度数为 ．12. 点A（1，﹣2）关于x轴对称的点的坐标是 ．13. 分解因式：2a2﹣4a＝ ．14. 如图，在△ABC中，BC＝5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是cm．
15. 如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是 ．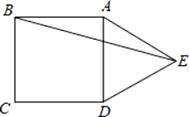
16. 如图，已知△ABC中，AB＝AC＝16cm，∠B＝∠C，BC＝10cm，点D为AB的中点，如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若当△BPD与△CQP全等时，则点Q运动速度可能为厘米/秒．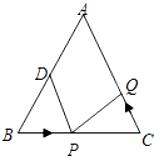
三、解答题（一）（共18分）
-
17. 计算：4x3•x﹣（x2）2﹣（2019﹣π）0+2x7÷x318. 解方程： ﹣ ＝219. 如图，AD、BC相交于点O，AD＝BC，∠C＝∠D＝90°．
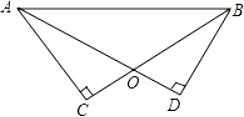(1)、求证：△ACB≌△BDA；(2)、若∠ABC＝32°，求∠CAO的度数．四、解答题（二）（共21分）
-
20. 在△ABC中，∠C＝90°
(1)、尺规作图：作AB的垂直平分线，交BC于点D，交AB于点E；（不写作法图，保留作图痕迹）(2)、若AC＝2，∠B＝15°，求BD的长．21. 先化简，再求值：（1+ ）÷ ，然后从0＜x≤3的范围内选取一个合适的整数作为x的值代入求值．22. 小张从家出发去距离9千米的婆婆家，他骑自行车前往比乘汽车多用20分钟，乘汽车的平均速度是骑自行车的3倍，求小张骑自行车的平均速度．五、解答题（三）（共27分）
-
23. 阅读材料：常用的分解因式方法有提取公因式法、公式法等，但有的多项式只用上述方法就无法分解，如x2﹣4y2﹣2x+4y，细心观察这个式子会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式，过程为：
x2﹣4y2﹣2x+4y＝（x2﹣4y2）﹣（2x﹣4y）
＝（x+2y）（x﹣2y）﹣2（x﹣2y）
＝（x﹣2y）（x+2y﹣2）
这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：
(1)、分解因式x2﹣2xy+y2﹣25；(2)、△ABC三边a，b，c满足a2﹣ab﹣ac+bc＝0，判断△ABC的形状．24. 在△BC中，∠ACB＝90°，AC＝BC，点D是AB的中点，点E是AB边上一点．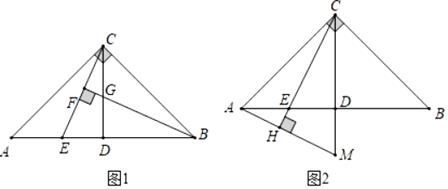
(1)、直线BF垂直于CE于点F，交CD于点G（如图1）．求证：AE＝CG；(2)、直线AH垂直于CE，垂足为H，交CD的延长线于点M（如图2）．试猜想CM与BE有怎样的数量和位置关系？并证明你的猜想．25. 如图，△ABC中，AB＝BC＝AC＝24cm，现有两点M、N分别从点A、点B同时出发，沿三角形的边运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M、N同时停止运动．
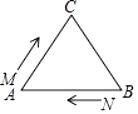(1)、点M，N运动几秒后，M、N两点重合？(2)、点M、N运动几秒后，可得到等边三角形△AMN？(3)、当点M、N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M、N运动的时间．