2016-2017学年江西省抚州市崇仁县七年级上学期期中数学试卷
试卷更新日期:2017-05-16 类型:期中考试
一、选择题:
-
1. 的绝对值是( )A、 B、 C、2 D、﹣22. 下列图形经过折叠不能围成棱柱的是( )A、
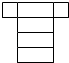 B、
B、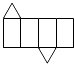 C、
C、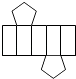 D、
D、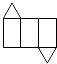 3. 我国成功发射了嫦娥三号卫星,是世界上第三个实现月面软着陆和月面巡视探测的国家,嫦娥三号探测器的发射总质量约为3700千克,3700用科学记数法表示为( )A、3.7×102 B、3.7×103 C、37×102 D、0.37×1044. 下列各式中,不是同类项的是( )A、 x2y和 x2y B、﹣ab和ba C、﹣ abcx2和﹣ x2abc D、 x2y和 xy35. 有理数a,b在数轴上的位置如图所示,则下列各式:
3. 我国成功发射了嫦娥三号卫星,是世界上第三个实现月面软着陆和月面巡视探测的国家,嫦娥三号探测器的发射总质量约为3700千克,3700用科学记数法表示为( )A、3.7×102 B、3.7×103 C、37×102 D、0.37×1044. 下列各式中,不是同类项的是( )A、 x2y和 x2y B、﹣ab和ba C、﹣ abcx2和﹣ x2abc D、 x2y和 xy35. 有理数a,b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0.一定成立的是( )
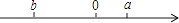 A、①②③ B、③④ C、②③④ D、①③④6.
A、①②③ B、③④ C、②③④ D、①③④6.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
 A、38 B、52 C、66 D、74
A、38 B、52 C、66 D、74二、填空题:
-
7. 化简x﹣y﹣(x+y)的最后结果是 .8. 已知甲地的海拔高度是300m,乙地的海拔高度是﹣50m,那么甲地比乙地高 m.9. 单项式 的系数是 , 次数是 .10. 在数轴上与﹣1相距3个单位长度的点表示的有理数是 .11.
若要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之和为6,则x+y= .
 12.
12.如图是小明用火柴搭的1条、2条、3条“金鱼”…,则搭n条“金鱼”需要火柴根.
 13. 若|a+5|+(b﹣4)2=0,则(a+b)2009= .14. 已知|a|=5,|b|=7,且|a+b|=a+b,则a•b的值为 .
13. 若|a+5|+(b﹣4)2=0,则(a+b)2009= .14. 已知|a|=5,|b|=7,且|a+b|=a+b,则a•b的值为 .三、解答题
-
15. 计算:(1)、(﹣36)×( ﹣ ﹣ )(2)、﹣14﹣5×(﹣ )÷(﹣ )16. 化简:(1)、﹣3m+2m﹣5m(2)、(2a2﹣1+2a)﹣(a﹣1+a2)17. 画出数轴,在数轴上表示下列各数,并用“<”连接:+5,﹣3.5, , ,4,0,2.5.18.
图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
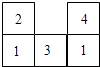 19. 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
19. 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题: (1)、用含x、y的代数式表示地面总面积;(2)、若x=5,y= ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?20. 一辆货车为一家商场的仓库运货,仓库在记录进出货物时把运进记作正数,运出记作负数下午记录如下(单位:吨):5.5,﹣4.6,﹣5.3,5.4,﹣3.4,4.8,﹣3(1)、仓库上午存货物60吨,下午运完货物后存货多少吨?(2)、如果货车的运费为每吨10元,那么下午货车共得运费多少元?21. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)、用含x、y的代数式表示地面总面积;(2)、若x=5,y= ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?20. 一辆货车为一家商场的仓库运货,仓库在记录进出货物时把运进记作正数,运出记作负数下午记录如下(单位:吨):5.5,﹣4.6,﹣5.3,5.4,﹣3.4,4.8,﹣3(1)、仓库上午存货物60吨,下午运完货物后存货多少吨?(2)、如果货车的运费为每吨10元,那么下午货车共得运费多少元?21. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
 (1)、当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);(2)、分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.22. 已知a是最大的负整数,b是多项式2m2n﹣m3n2﹣m﹣2的次数,c是单项式﹣2xy2的系数,且a、b、c分别是点A、B、C在数轴上对应的数.(1)、求a、b、c的值,并在数轴上标出点A、B、C.
(1)、当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);(2)、分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.22. 已知a是最大的负整数,b是多项式2m2n﹣m3n2﹣m﹣2的次数,c是单项式﹣2xy2的系数,且a、b、c分别是点A、B、C在数轴上对应的数.(1)、求a、b、c的值,并在数轴上标出点A、B、C. (2)、若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?(3)、在数轴上找一点M,使点M到A、B、C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由).23. 观察下列等式 =1﹣ , = ﹣ , = ﹣ ,将以这三个等式两边分别相加得: + + =1﹣ + ﹣ + ﹣ =1﹣ = .(1)、猜想并写出: = .(2)、直接写出下列各式的计算结果: + + +…+ = .(3)、探究并计算: + + +…+ .
(2)、若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?(3)、在数轴上找一点M,使点M到A、B、C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由).23. 观察下列等式 =1﹣ , = ﹣ , = ﹣ ,将以这三个等式两边分别相加得: + + =1﹣ + ﹣ + ﹣ =1﹣ = .(1)、猜想并写出: = .(2)、直接写出下列各式的计算结果: + + +…+ = .(3)、探究并计算: + + +…+ .