2016-2017学年湖北省武汉市青山区七年级上学期期中数学试卷

试卷更新日期：2017-05-16 类型：期中考试

进入出卷网下载

一、一.选择题

1. 向东行驶3km，记作+3km，向西行驶2km记作（）

A、+2km B、﹣2km C、+3km D、﹣3km

查看试题解析
2. ﹣3的绝对值是（）

A、3 B、±3 C、﹣3 D、 $\frac{1}{3}$

查看试题解析
3. ﹣ $\frac{1}{5}$ 的倒数是（）

A、 $\frac{1}{5}$ B、﹣ $\frac{1}{5}$ C、﹣5 D、5

查看试题解析
4. 下列各组式中，为同类项的是（）

A、3x²y与﹣3xy² B、3xy与﹣2yx C、2x与2x² D、7xy与7yz

查看试题解析
5. 下列各式成立的是（）

A、a﹣（b+c）=a﹣b+c B、a+b﹣c=a+（b﹣c） C、a+（b+c）=a﹣b+c D、a+b﹣c=a﹣（b+c）

查看试题解析
6. 单项式﹣ $\frac{2 a^{2} b}{3}$ 的系数与次数分别是（）

A、﹣2，2 B、﹣2，3 C、 $\frac{2}{3}$ ，3 D、﹣ $\frac{2}{3}$ ，3

查看试题解析
7. 下列各式的计算结果正确的是（）

A、2x+3y=5xy B、5x﹣3x=2x² C、7y²﹣5y²=2 D、9a²b﹣4ba²=5a²b

查看试题解析
8. 下列各对数中，数值相等的是（）

A、2³和3² B、（﹣2）²和﹣2² C、﹣（﹣2）和|﹣2| D、 ${(\frac{2}{3})}^{2}$ 和 $\frac{2^{2}}{3}$

查看试题解析
9. 有理数a，b在数轴上的对应位置如图，则下列结论正确的是（）

A、ab＞0 B、 $\frac{a}{b}$ ＜0 C、a+b＜0 D、a﹣b＜0

查看试题解析
10. 下列说法正确的个数有（）
①若干个不为0的有理数相乘，积的符号由负因数的个数决定；②两个四次多项式的和一定是四次多项式；③若a大于b，则a的倒数小于b的倒数；④若xyz＜0，则 $\frac{| x |}{x} + \frac{| y |}{y} + \frac{| z |}{z} + \frac{| x y z |}{x y z}$ 的值为0或﹣4．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、二.填空题

11. ﹣7的相反数是．

查看试题解析
12. 我国的南海资源丰富，其面积为3500000平方千米，相当于渤海、黄海和东海总面积的3倍．其中3500000用科学记数法可表示为．

查看试题解析
13. 多项式 $\frac{2}{3}$ x⁴﹣ $\frac{4}{5}$ x²﹣x﹣1的次数、项数、常数项分别为．

查看试题解析
14. 下列整式中： $\frac{m^{4} n^{2}}{7}$ 、﹣ $\frac{1}{2}$ x²y、x²+y²﹣1、x、3x²y+3xy²+x⁴﹣1、32t³、2x﹣y，单项式的个数为a，多项式的个数为b，则ab= ．

查看试题解析
15. 已知代数式x﹣2y的值是 $\frac{1}{2}$ ，则代数式﹣2x+4y﹣1的值是．

查看试题解析
16. 观察表一，寻找规律，表二、表三、表四分别是从表一中截取的一部分，则a﹣b+m= ．

查看试题解析

三、三.解答题.

17. 计算：

(1)、12﹣（﹣18）+（﹣7）

(2)、﹣2³÷（﹣ $\frac{1}{8}$ ）﹣ $\frac{1}{4}$ ×（﹣2）² ．

查看试题解析
18. 计算：

(1)、3xy﹣4xy﹣（﹣2xy）

(2)、5（3a²b﹣ab²）﹣3（ab²﹣2a²b）

查看试题解析
19. 邮递员从邮局出发，先向西骑行3km到达A村，继续骑行2km到达B村，然后向东行骑行9km到达C村，最后回到邮局．

(1)、如图，请在以邮局为原点，向东为正方向，1km为1个单位长度的数轴上表示出A、B、C三个村庄的位置；

(2)、C村离A村有多远？

(3)、邮递员一共行驶了多少千米？

查看试题解析
20. 化简求值： $\frac{1}{2}$ x﹣2（x﹣ $\frac{1}{3}$ y²）+（﹣ $\frac{3}{2}$ x+ $\frac{1}{3}$ y²），其中|x+2|+（3y﹣2）²=0．

查看试题解析
21. 某商店有一种商品每件成本a元，原来成本增加22%定价售价，售出80件后，由于库存积压减价，按原来的85%出售，又增加120件．

(1)、求该商品减价后的售价价格为多少元？

(2)、售完200件这种商品是盈利还是亏损？若盈利共盈利了多少元？若亏损共亏损了多少元？

查看试题解析
22. 综合题。

(1)、任取一个两位数，十位数字记作a，个位数字记作b，交换a和b的位置，得到一个新的两位数，则新两位数与原两位数的和一定能被整除．

(2)、任取一个三位数M，百位数字记作a，十位数字记作b，个位数字记作c，且使a﹣c＞1，对这个三位数M进行如下操作：
①交换a和c的位置，构成一个新的三位数（记作N）．请用含a、b、c的式子分别表示数N和M﹣N；

查看试题解析
23.
幻方的历史很悠久，传统幻方最早出现在下雨时代的“洛书”．“洛书”用今天的数学符号翻译出来，就是一个三阶幻方，如图1所示．

(1)、①请你依据“洛书”把1，2，3，5，8填入如图2剩余的方格中使每横行、每竖列以及两条对角线上的数的和都是15；②把﹣4，﹣3，﹣2，﹣1，0，1，2，3，4填入如图2的方格中，使每横行、每竖列以及两条对角线上的数的和都相等；

(2)、若把2x﹣4，2x﹣3，2x﹣2，2x﹣1，2x，2x+1，2x+2，2x+3，2x+4填入如图3的方格中，使每横行、每竖列以及两条对角线上的数的和都相等，则每行的和是（用含x的式子表示）

(3)、根据上述填数经验，请把3² ， 3⁴ ， 3⁶ ， 3⁸ ， 3¹⁰ ， 3¹² ， 3¹⁴ ， 3¹⁶ ， 3¹⁸填入如图4的方格中，使每横行、每竖列以及两条对角线上的数的积都相等．

查看试题解析
24. 如图，数轴上A、B两点对应的有理数分别为20和30，点P和点Q分别同时从点A和点O出发，以每秒2个单位长度，每秒4个单位长度的速度向数轴正方向运动，设运动时间为t秒．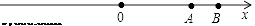

(1)、当t=2时，则P、Q两点对应的有理数分别是；PQ=；

(2)、点C是数轴上点B左侧一点，其对应的数是x，且CB=2CA，求x的值；

(3)、在点P和点Q出发的同时，点R以每秒8个单位长度的速度从点B出发，开始向左运动，遇到点Q后立即返回向右运动，遇到点P后立即返回向左运动，与点Q相遇后再立即返回，如此往返，直到P、Q两点相遇时，点R停止运动，求点R运动的路程一共是多少个单位长度？点R停止的位置所对应的数是多少？

查看试题解析