2017年浙江省永康市初中毕业生适应性考试数学卷
试卷更新日期:2017-05-16 类型:中考模拟
一、一、选择题
-
1. -2017的相反数是( )A、 B、2017 C、-2017 D、-2.
如图,已知a∥b,∠1=68°,则∠2=( )
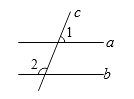 A、22° B、68° C、102° D、112°3. 抛物线 先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )A、 B、 C、 D、4. 下列运算正确的是 ( )A、 B、 C、 D、5.
A、22° B、68° C、102° D、112°3. 抛物线 先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )A、 B、 C、 D、4. 下列运算正确的是 ( )A、 B、 C、 D、5.如图物体的主视图是( )
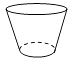 A、
A、 B、
B、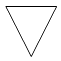 C、
C、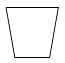 D、
D、 6. 分式方程 的解是( )A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别在AB,AC上,且 ,则 : ( )
6. 分式方程 的解是( )A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别在AB,AC上,且 ,则 : ( )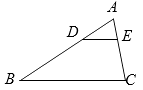 A、1:2 B、1:4 C、1:8 D、1:98. 某校7个班同学积极捐出自己的零花钱献爱心,各班捐款的数额分别是(单位:元):500,200,500,300,500,250,1350.这组数据的众数和中位数分别是( )A、500,200 B、500,500 C、500,300 D、1350,5009. 不等式组 的解在数轴上表示为 ( )A、
A、1:2 B、1:4 C、1:8 D、1:98. 某校7个班同学积极捐出自己的零花钱献爱心,各班捐款的数额分别是(单位:元):500,200,500,300,500,250,1350.这组数据的众数和中位数分别是( )A、500,200 B、500,500 C、500,300 D、1350,5009. 不等式组 的解在数轴上表示为 ( )A、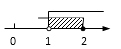 B、
B、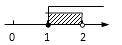 C、
C、 D、
D、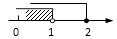 10. 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
10. 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )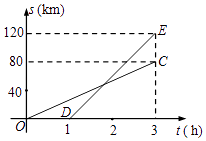 A、乙到达B地时甲距A地120km B、乙出发1.8小时被甲追上 C、甲,乙相距20km时,t为2.4h D、甲的速度是乙的速度的 倍
A、乙到达B地时甲距A地120km B、乙出发1.8小时被甲追上 C、甲,乙相距20km时,t为2.4h D、甲的速度是乙的速度的 倍二、填空题
-
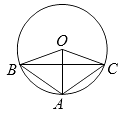
11. 因式分解: =.12. 函数 自变量x的取值范围是 .13. 如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC= .
 14. 一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是 .15. 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE,若点A到CE的距离为17,则CE= .
14. 一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是 .15. 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE,若点A到CE的距离为17,则CE= .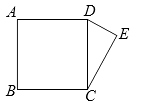 16. 一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小
16. 一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包
贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的
侧面展开进行分析.
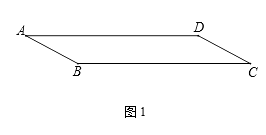
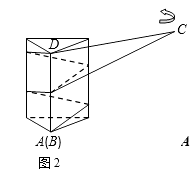
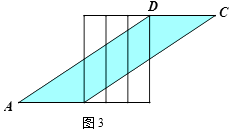 (1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm.
(1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm.三、解答题
-
17. 计算:18. 先化简,再求值:
,其中x=2.
19.如图所示,在▱ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
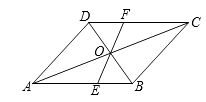 (1)、求证:OE=OF;(2)、若AB=6,BC=5,OE=2,求四边形BCFE的周长.20. 小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
(1)、求证:OE=OF;(2)、若AB=6,BC=5,OE=2,求四边形BCFE的周长.20. 小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.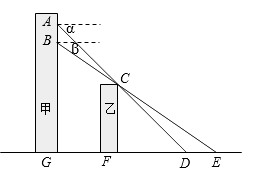 (1)、求点A到地面的距离AG;(2)、求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)21.
(1)、求点A到地面的距离AG;(2)、求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)21.学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
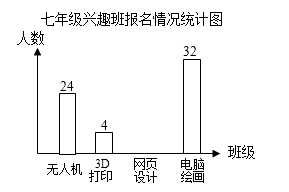
七年级兴趣班报名情况统计表
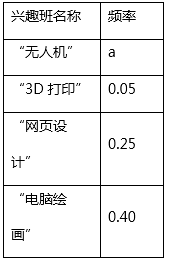 (1)、报名参加兴趣班的总人数为人;统计表中的a=;(2)、将统计图补充完整;(3)、为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?22. 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)、报名参加兴趣班的总人数为人;统计表中的a=;(2)、将统计图补充完整;(3)、为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?22. 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.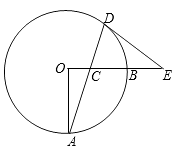 (1)、求证:∠ECD=∠EDC;(2)、若tanA= ,求DE长;(3)、当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.23. 综合题(1)、探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
(1)、求证:∠ECD=∠EDC;(2)、若tanA= ,求DE长;(3)、当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.23. 综合题(1)、探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a , b).
①若 ,请用含n的代数式表示 ;
②求证: ;
(2)、应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数 的图象交于点C,D两点(点C在点D的左边),已知 ,△OBD的面积为1,试用含m的代数式表示k.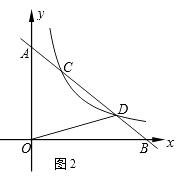 24. 已知,抛物线y=ax²+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
24. 已知,抛物线y=ax²+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.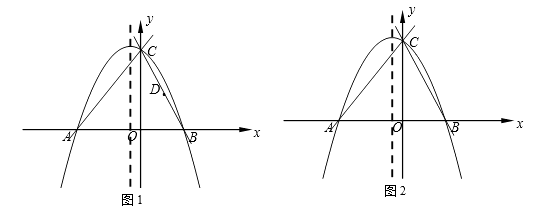 (1)、求抛物线的解析式;(2)、如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;(3)、如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线
(1)、求抛物线的解析式;(2)、如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;(3)、如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.