浙江省湖州市南浔区2018-2019学年九年级下学期数学中考一模试卷
试卷更新日期:2019-04-30 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
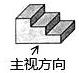
1. 在0,1,-3,-1四个数中,最小的数是( )A、0 B、1 C、-3 D、-12. 解不等式2x>6,正确的是( )A、x<4 B、x>4 C、x<3 D、x>33. 一组数据2,3,5,4,4,6的众数和平均数分别是( )A、4.5和4 B、4和4 C、4和4.8 D、5和44. 某移动台阶如图所示,它的主视图是( )
 A、
A、 B、
B、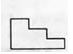 C、
C、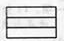 D、
D、 5. 如图,已知点A,B,C在⊙O上,若∠ABC=130°,则∠AOC的度数是( )
5. 如图,已知点A,B,C在⊙O上,若∠ABC=130°,则∠AOC的度数是( )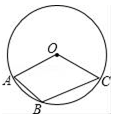 A、50° B、60° C、80° D、100°6. 若命题“关于x的一元二次方程x2+bx+1=0有实数解”是假命题,b的值可以是( )A、-3 B、-2 C、-1 D、27. 小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )
A、50° B、60° C、80° D、100°6. 若命题“关于x的一元二次方程x2+bx+1=0有实数解”是假命题,b的值可以是( )A、-3 B、-2 C、-1 D、27. 小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )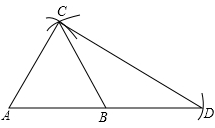
A、∠A=60° B、△ACD是直角三角形(第,爱画) C、BC= CD D、点B是△ACD的外心8. 如图,已知一个函数的图象由曲线AB,线段BC,射线CD组成,其中点A(-3,2),B(3,6),C(5,1),D(10,10),则此函数( )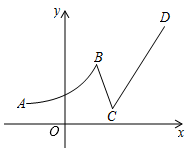
A、当x<3时,随x的增大面增大 B、当x<3时,y随x的增大而减小 C、当x>3时,随x的增大面增大 D、当x>3时,随x的增大而减小9. 如图,已知在平行四边形ABCD中,BD=BC,点E是AB的中点,连结DE并延长,与CB的延长线相交于点F,连结AF.若AD=5,tan∠BDC=2,则四边形AFBD的面积是( )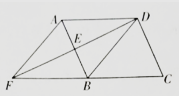 A、20 B、 C、10 D、10. 已知A,B两地相距300千米,甲骑摩托车从A地出发匀速驶向B地当甲行驶lh后,乙骑自行车以20km/h的速度从B地出发匀速驶向A地.甲到达B地后马上以原速按原路返回,直至甲追上乙。在此过程中,甲、乙两人之间的距离y(km)与甲行驶时间x(h)之间的函数关系如图所示。下列说法;①甲最终追上乙时,乙骑行了7小时;②点P的纵坐标为240;③线段QM所在直线的解析式为y=40x-160;④当x= 时,甲、乙两人之间相距60千米。其中说法正确的序号是( )
A、20 B、 C、10 D、10. 已知A,B两地相距300千米,甲骑摩托车从A地出发匀速驶向B地当甲行驶lh后,乙骑自行车以20km/h的速度从B地出发匀速驶向A地.甲到达B地后马上以原速按原路返回,直至甲追上乙。在此过程中,甲、乙两人之间的距离y(km)与甲行驶时间x(h)之间的函数关系如图所示。下列说法;①甲最终追上乙时,乙骑行了7小时;②点P的纵坐标为240;③线段QM所在直线的解析式为y=40x-160;④当x= 时,甲、乙两人之间相距60千米。其中说法正确的序号是( )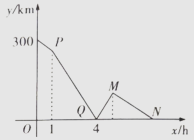 A、①③ B、①④ C、②③ D、②④
A、①③ B、①④ C、②③ D、②④二、填空题(本题有6小题,每小题4分,共24分)
-
11. 2019的相反数是 。12. 把多项式a2-3a因式分解,正确的结果是。
13. 五张扑克牌中有两张红桃,把它们背面朝上,从中任抽一张,则抽到红桃的概率是。14. 如图,已知某商店营业大厅自动扶梯AB的倾斜角为31°,自动扶梯AB的长为10米,则大厅两层之间的高度BC为米。【参考数据;sin31°=0.515,cn31°=0.857,tan31°=0.601】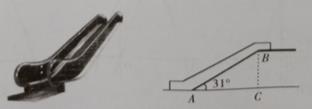 15. 如图,已知在矩形0ABC中,0A=3,OC=2,以边OA,OC所在的直线为轴建立平面直角坐标系xOy,反比例函数y= (x>0)的图象经过点B,点P(t,0)是x轴正半轴上的动点,将点B绕点P顺时针旋转90°,使点B恰好落在反比例y= (x>0)的图象上,则t的值是。
15. 如图,已知在矩形0ABC中,0A=3,OC=2,以边OA,OC所在的直线为轴建立平面直角坐标系xOy,反比例函数y= (x>0)的图象经过点B,点P(t,0)是x轴正半轴上的动点,将点B绕点P顺时针旋转90°,使点B恰好落在反比例y= (x>0)的图象上,则t的值是。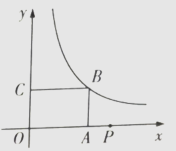 16. 如图,已知在△ABC中,∠ACB=90°,AC=4,BC=3,动点N从点C出发,沿着CA方向以1个单位长度/秒的速度匀速运动,同时动点M从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤2.5),以M为圆心,MA长为半径的⊙M与AB的另一个交点为点D,连结DN.当OM与线段DN只有一个公共B点时,t的取值范围是 。
16. 如图,已知在△ABC中,∠ACB=90°,AC=4,BC=3,动点N从点C出发,沿着CA方向以1个单位长度/秒的速度匀速运动,同时动点M从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤2.5),以M为圆心,MA长为半径的⊙M与AB的另一个交点为点D,连结DN.当OM与线段DN只有一个公共B点时,t的取值范围是 。
三、解答题(本题有8小题,共66分)
-
17. 计算:18. 已知x与y成反比例,且当x=-2时,y=3.(1)、求y关于x的函数解析式;(2)、当x=-1时,求y的值19. 如图,在方格纸中,每个小正方形的边长都是1,点A,B,P都在格点上,请按要求画出图形,使P在所画图形内部(不包括边界上).
 (1)、在图甲中画出一个面积是3的△ABC,点C在格点上;(2)、在图乙中画出一个四边形ABCD,使BC=CD,且∠A是锐角,点C.D在格点上。20. 某校社团活动开设的体育选修课有:篮球(A),足球(B),排球(C),羽毛球(D),乒乓球(E).每个学生选修其中的一门.学校对学生体育选修课的选课情况进行抽样调查,调查统计后制成了以下两个统计图(不完整).
(1)、在图甲中画出一个面积是3的△ABC,点C在格点上;(2)、在图乙中画出一个四边形ABCD,使BC=CD,且∠A是锐角,点C.D在格点上。20. 某校社团活动开设的体育选修课有:篮球(A),足球(B),排球(C),羽毛球(D),乒乓球(E).每个学生选修其中的一门.学校对学生体育选修课的选课情况进行抽样调查,调查统计后制成了以下两个统计图(不完整). (1)、求抽样调查的学生总数;(2)、求出选修篮球(A)和乒乓球(E)的人数,并补全条形统计图;(3)、该校共有850名学生,请估计该校学生体育选修课选修篮球(A)的学生约有多少人?21. 如图,已知AB,CD是⊙O的两条直径,AE∥CD交⊙O于点E,连结BE交CD于点F.
(1)、求抽样调查的学生总数;(2)、求出选修篮球(A)和乒乓球(E)的人数,并补全条形统计图;(3)、该校共有850名学生,请估计该校学生体育选修课选修篮球(A)的学生约有多少人?21. 如图,已知AB,CD是⊙O的两条直径,AE∥CD交⊙O于点E,连结BE交CD于点F. (1)、求证: ;(2)、若⊙O的半径为6,AE=6 ,求图中阴影部分的面积22. 2018年,在南得区美丽乡村建设中,甲、乙两个工程队分别承担村级道路硬化和道路拓宽改造工程已知道路硬化和道路拓宽改造工程的总里程数是8.6千米,其中道路硬化的里程数是道路拓宽里程数的2倍少1千米(1)、求道路硬化和道路拓宽里程数分别是多少千米;(2)、甲、乙两个工程队同时开始施工,甲工程队比乙工程队平均每天多施工10米。由于工期需要,甲工程队在完成所承担的 施工任务后,通过技术改进使工作效率比原来提高了 。设乙工程队平均每天施工a米,请回答下列问题。
(1)、求证: ;(2)、若⊙O的半径为6,AE=6 ,求图中阴影部分的面积22. 2018年,在南得区美丽乡村建设中,甲、乙两个工程队分别承担村级道路硬化和道路拓宽改造工程已知道路硬化和道路拓宽改造工程的总里程数是8.6千米,其中道路硬化的里程数是道路拓宽里程数的2倍少1千米(1)、求道路硬化和道路拓宽里程数分别是多少千米;(2)、甲、乙两个工程队同时开始施工,甲工程队比乙工程队平均每天多施工10米。由于工期需要,甲工程队在完成所承担的 施工任务后,通过技术改进使工作效率比原来提高了 。设乙工程队平均每天施工a米,请回答下列问题。①根据题意,填写下表;
乙工程队
甲工程队
技术改进前
技术改进后
施工天数(天)(用含a的代数式表示)
②若甲、乙两队同时完成施工任务,求乙工程队平均每天施工的米数a和施工的天数
23. 如图1,已知在平面直角坐标系xOy中,抛物线y=-x2-2x+c(c>0)的图象与x轴交于A,B两点,与y轴交于点C.抛物线的顶点为E,若点B的坐标是(1,0),点D是该抛物线在第二象限图象上的一个动点。 (1)、求该抛物线的解析式和顶点E的坐标;(2)、设点D的横坐标是a,问当a取何值时,四边形AOCD的面积最大;(3)、如图2,若直线0D的解析式是y=-3x,点P和点0分别在抛物线上和直线OD上,问:是否存在以点P,Q,O,C为顶点的四边形是平行四边形?若存在,请求出符合题意的点Q的坐标;若不存在,请说明理由。24. 我们定义:如果一个三角形一条边上的高等于这条边的两倍,那么这个三角形叫做“倍高底”三角形,这条边叫做这个三角形的“倍底”。
(1)、求该抛物线的解析式和顶点E的坐标;(2)、设点D的横坐标是a,问当a取何值时,四边形AOCD的面积最大;(3)、如图2,若直线0D的解析式是y=-3x,点P和点0分别在抛物线上和直线OD上,问:是否存在以点P,Q,O,C为顶点的四边形是平行四边形?若存在,请求出符合题意的点Q的坐标;若不存在,请说明理由。24. 我们定义:如果一个三角形一条边上的高等于这条边的两倍,那么这个三角形叫做“倍高底”三角形,这条边叫做这个三角形的“倍底”。 (1)、【概念理解】
(1)、【概念理解】如图1,在正方形ABCD中,点E是BC的中点,试判断△ABE是否是“倍高底”三角形,请说明理由;
(2)、【问题探究】如图2,钝角△ABC是“倍高底”三角形,BC是“倍底”,∠B=450,AC=2 ,求BC的长;
(3)、【应用拓展】如图3,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一点,D是PB的中点,过点A,M,D的圆与BP交于另一点C,连结AC.当△PAB是“倍高底”三角形时,求△ABC的面积。