浙江省杭州市余杭区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-04-30 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. 下列交通标志中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{9} = 3$ B、 ${(- \sqrt{3})}^{2} = - 3$ C、 $\sqrt{{(- 6)}^{2}} = \pm 6$ D、 ${(\sqrt{7})}^{2} = - 7$

查看试题解析
3. 二次根式 $\sqrt{1 - x}$ 有意义的x的范围是（）

A、x＝1 B、x≠1 C、x≥1 D、x≤1

查看试题解析
4. 若多边形的边数由3增加到n(n为大于3的正整数)，则其外角和的度数（）

A、增加 B、减少 C、不变 D、不能确定

查看试题解析
5. 下列二次根式中能与2 $\sqrt{3}$ 合并的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{18}$ D、 $\sqrt{9}$

查看试题解析
6. 一组数据1，2，3，4，4，10．去掉10，剩下的数据原数据相比，不变的是（）

A、平均数 B、中位数 C、众数 D、平均数和众数

查看试题解析
7. 平行四边形一边的长是10cm，则这个平行四边形的两条对角线长可以是（）

A、4cm或6cm B、6cm或8cm C、8cm或12cm D、20cm或30cm

查看试题解析
8. 如果一元二次方程ax²＋bx＋c＝0(a≠0)满足4a－2b＋c＝0，且有两个相等的实数根，则（）

A、b＝a B、c＝2a C、a(x＋2)²＝0(a≠0) D、a(x－2)²＝0(a≠0)

查看试题解析
9. 欧几里得的《原本》记载，形如x²＋ax＝b²的方程的图解法是：
画Rt△ABC，使∠ACB＝90°，BC＝ $\frac{a}{2}$ ，AC＝b，再在斜边AB上截取BD＝ $\frac{a}{2}$ ．

则该方程的一个正根是（）

A、AC的长 B、CD的长 C、AD的长 D、BC的长

查看试题解析
10. 如图，在平行四边形ABCD中，∠B＜90°，BC＞AB．作AE⊥BC于点E，AF⊥CD于点F，记∠EAF的度数为α，AE＝a，AF＝b．则以下选项错误的是（）

A、∠D的度数为α B、a∶b＝CD∶BC C、若α＝60°，则平行四边形ABCD的周长为 $\frac{4}{3} \sqrt{3} (a + b)$ D、若α＝60°，则四边形AECF的面积为平行四边形ABCD面积的一半

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

11. 化简 $\frac{1}{\sqrt{5}}$ ＝．

查看试题解析
12. 一组数据1，3，5，7，9的方差为．

查看试题解析
13. 某校5个假日小队参加植树活动，平均每组植树10株．已知第一、二、三、五组分别植树9株、12株、9株、8株，则第四小组植树株．

查看试题解析
14. 已知一个一元二次方程的二次项系数是2，常数项是－14，它的一个根是－7，则这个方程为．

查看试题解析
15. 如图，在平行四边形ABCD中，E，F分别为AB，BC的中点，G是AD 上的任一点．计S₁＝S_△_BEF ， S₂＝S_△_GFC ， S＝S_□_ABCD ，则S＝S₂＝S₁ ．

查看试题解析
16. 商场某种商品进价为120元/件，售价130元/件时，每天可销售70件；售价单价高于130元时，每涨价1元，日销售量就减少1件．据此，若售价单价为元，商场每天盈利达1500元；该商场销售这种商品日最高利润为元．

查看试题解析

三、解答题：本题有7小题，共66分．

17. 解方程：

(1)、x(2x－7)＝2x

(2)、 $2 x^{2} + 4 x - 3 = 0$

查看试题解析
18. 计算或求值：

(1)、计算： (1－ )－

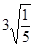(2)、已知a＝＋，b＝－，求a²－ab＋b²的值．

查看试题解析
19. 如图是某校在慈善爱心捐款活动中的统计情况，图1是各年级捐款人数占总捐款人数的百分比，图2是对部分学生捐款金额和人数的抽样调查．

(1)、在抽取的样本中，捐款金额的平均数、中位数、众数各是多少？

(2)、若该校九年级共有200人捐款，请你估计全校捐款的总金额约为多少元？

查看试题解析
20. 如图，平行四边形ABCD中，AP，BP分别平分∠DAB和∠CBA，交于DC边上点P，AD＝5．

(1)、求线段AB的长．

(2)、若BP＝6，求△ABP的周长．

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} + (m - 5) x - 5 m = 0$ ．

(1)、求证：这个一元二次方程一定有两个实数根．

(2)、设该一元二次方程的两根为a，b，且2，a，b分别是一个直角三角形的三边长，求m的值．

查看试题解析
22. 在△ABC中，AB＝AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E，构造出平行四边形AEDF．

(1)、若点D在线段BC上时．
①求证：FB＝FD．②求证：DE＋DF＝AC．

(2)、点D在边BC所在的直线上，若AC＝8，DE＝3，请作出简单示意图求DF的长度，不需要证明．

查看试题解析
23. 方方同学在寒假社会调查实践活动中，对某罐头加工厂进行采访，获得了该厂去年的部分生产信息如下：
①该厂一月份罐头加工量为a吨；

②该厂三月份的加工量比一月份增长了44％；

③该厂第一季度共加工罐头182吨；

④该厂二月、三月加工量每月按相同的百分率增长；

⑤该厂从四月份开始设备整修更新，加工量每月按相同的百分率开始下降；

⑥六月份设备整修更新完毕，此月加工量为一月份的2.1倍，与五月份相比增长了46.68吨．

利用以上信息求：

(1)、该厂第一季度加工量的月平均增长率；

(2)、该厂一月份的加工量a的值；

(3)、该厂第二季度的总加工量．

查看试题解析