浙江省杭州市余杭区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-04-30 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. x²·x³的结果是（）

A、x⁵ B、x⁶ C、5x D、2x²

查看试题解析
2. 如图中，∠1的同位角是（）。

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
3. 下列多项式乘法中，能用平方差公式计算的是（）

A、 $(- m + n) (m - n)$ B、 $(\frac{1}{2} a + b) (b - \frac{1}{2} a)$ C、 $(x + 5) (x + 5)$ D、 $(3 a - 4 b) (3 b - 4 a)$

查看试题解析
4. 如图，将△ABC沿着某一方向平移一定的距离得到△DEF，则下列结论：
①AD＝CF；②AC∥DF；③∠ABC＝∠DFE；④∠DAE＝∠AEB．正确的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 下列各组数不是方程2x＋y＝20的解的是（）

A、 ${\begin{matrix} x = - 10 ， \\ y = 0 \end{matrix}$ B、 ${\begin{matrix} x = 1 ， \\ y = 18 \end{matrix}$ C、 ${\begin{matrix} x = - 1 ， \\ y = 22 \end{matrix}$ D、 ${\begin{matrix} x = 0 ， \\ y = 20 \end{matrix}$

查看试题解析
6. 以下运算结果是 $x^{2} + 1$ 的是（）

A、 ${(x + 1)}^{2}$ B、 $(x + 1) (x - 1)$ C、 ${(x - 1)}^{2} + 4 x$ D、 $(x^{2} + 2 x) - (2 x - 1)$

查看试题解析
7. 如图，点E在AC的延长线上，对于下列四个条件；①∠1＝∠2； ②∠3＝∠4；③∠A＝∠DCE；④∠D＋∠ABD＝180°．其中能判断AB∥CD的是（）

A、①③④ B、①②③ C、①②④ D、②③④

查看试题解析
8. 一辆轿车行驶2小时的路程比一辆卡车行驶3小时的路程少40千米．如果设轿车平均速度为a千米/小时，卡车的平均速度为b千米/小时，则（）

A、2a＝3b＋40 B、3b＝2a－40 C、2a＝3b－40 D、3b＝40－2a

查看试题解析
9. 如图，已知AB∥ED，设∠A＋∠E＝α，∠B＋∠C＋∠D＝β，则（）

A、α－β＝0 B、2α－β＝0 C、α－2β＝0 D、3α－2β＝0

查看试题解析
10. 对代数式(x＋3)² ，老师要求任意取一个x的值后求出代数式的值．圆圆发现，大家所求得的代数式的值都大于等于0，即x＝－3时代数式的最小值是0．利用这个发现，圆圆试着写出另外一些结论：①在x＝－3时，代数式(x＋3)²＋2的最小值为2；②在a＝－b时，代数式(a＋b)²＋m的最小值为m； ③ 在c＝－d时，代数式－(c＋d)²＋n的最大值为n；④ 在x＝－3时，代数式－x²－6x＋20的最大值为29．其中正确的为（）

A、①②③ B、①③ C、①④ D、①②③④

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

11. 已知2v＋t＝3v－2＝4，则v＝， t＝．

查看试题解析
12. 已知直线m∥n，将一块含有30º角的三角板ABC按如图所示的方式放置(∠ABC＝30°)，其中A，B两点分别落在直线m，n上．若∠1＝15º，则∠2＝º．

查看试题解析
13. 已知 $\frac{x}{3} - 2 y = 1$ ，用含x的代数式表示y为：y＝．

查看试题解析
14. 已知a^m＝4，aⁿ＝5，则 $a^{2 m + n}$ 的值是．

查看试题解析
15. 如图，直线a∥b，直线c，d与直线b相交于点A，∠3＝∠4，设∠1为α度，则∠2＝度(用含有α的代数式表示)．

查看试题解析
16. 若a－b＝3，ab＝2，则a²＋b²的值为；a＋b的值为．

查看试题解析

三、解答题：本题有7小题，共66分．

17. 化简：

(1)、 $(x + 1) (x + 2)$

(2)、 $2 a^{2} b \times (- 3 b c)$

查看试题解析
18. 解下列二元一次方程组：

(1)、

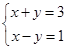(2)、 ${\begin{matrix} \frac{m + n}{3} - \frac{m - n}{4} = 3 ， \\ \frac{m + n}{2} - \frac{m - n}{3} = 5 \end{matrix}$

查看试题解析
19. 化简求值：

(1)、已知a＝ $\frac{1}{4}$ ，b＝－1，求(2a＋ $\frac{1}{2}$ b)(2a－ $\frac{1}{2}$ b)－a(4a－3b)的值．

(2)、已知x²－5x＝3，求2(x－1)(2x－1)－2(x＋1)²＋1的值．

查看试题解析
20. 已知如图，已知∠1＝∠2，∠C＝∠D．

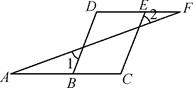(1)、判断BD与CE是否平行，并说明理由；

(2)、说明∠A＝∠F的理由．

查看试题解析
21. 一条高铁线A，B，C三个车站的位置如图所示．已知B，C两站之间相距530千米．高铁列车从B站出发，向C站方向匀速行驶，经过13分钟距A站165千米；经过80分钟距A站500千米．

(1)、求高铁列车的速度和AB两站之间的距离．

(2)、如果高铁列车从A站出发，开出多久可以到达C站？

查看试题解析
22. 一个长方形的长和宽分别为x厘米和y厘米（x，y为正整数），如果将长方形的长和宽各增加5厘米得到新的长方形，面积记为 $S_{1}$ ，将长方形的长和宽各减少2厘米得到新的长方形，面积记为 $S_{2}$ ．

(1)、请说明： $S_{1}$ 与 $S_{2}$ 的差一定是7的倍数．

(2)、如果 $S_{1}$ 比 $S_{2}$ 大196 $c m^{2}$ ，求原长方形的周长．

(3)、如果一个面积为 $S_{1}$ 的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形，请找出x与y的关系，并说明理由．

查看试题解析
23. 如图

(1)、如图1，将长方形纸片ABFE沿着线段DC折叠，CF交AD于点H，过点H作HG∥DC，交线段CB于点G．
①判断∠FHG与∠EDC是否相等，并说明理由；

②说明HG平分∠AHC的理由．

(2)、如图2，如果将(1)中的已知条件改为折叠三角形纸片ABE，其它条件不变．HG是否平分∠AHC？如果平分请说明理由；如果不平分，请找出∠CHG，∠AHG与∠E的数量关系并说明理由．

查看试题解析