浙教版2018-2019学年重点高中自主招生数学模拟试卷（六）

试卷更新日期：2019-04-29 类型：中考模拟

进入出卷网下载

一、选择题（共8小题，4*8=32）

1. 某火车站的显示屏，每间隔4分钟显示一次火车班次的信息，显示时间持续1分钟，某人到达该车站时，显示屏上正好显示火车班次信息的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
2. 中百超市推出如下优惠方案：（1）一次性购物不超过100元，不享受优惠；（2）一次性购物超过100元，但不超过300元一律9折；（3）一次性购物超过300元一律8折．王波两次购物分别付款80元、252元，如果他将这两次所购商品一次性购买，则应付款（）

A、288元 B、332元 C、288元或316元 D、332元或363元

查看试题解析
3. 使不等式x²＜|x|成立的x的取值范围是（）

A、x＞1 B、x＜﹣1 C、﹣1＜x＜1 D、﹣1＜x＜0或0＜x＜1

查看试题解析
4. 如图，P（x，y）是以坐标原点为圆心，5为半径的圆周上的点，若P都是整数点，则这样的点共有（）

A、4个 B、8个 C、12个 D、16个

查看试题解析
5. 抛物线y=ax²与直线x=1，x=2，y=1，y=2围成的正方形有公共点，则实数a的取值范围是（　　）

A、 $\frac{1}{4}$ ≤a≤1 B、 $\frac{1}{2}$ ≤a≤2 C、 $\frac{1}{2}$ ≤a≤1 D、 $\frac{1}{4}$ ≤a≤2

查看试题解析
6. 若A（a，b），B（ $\frac{1}{a}$ ，c）两点均在函数y＝ $\frac{1}{x}$ 的图象上，且﹣1＜a＜0，则b﹣c的值为（）

A、正数 B、负数 C、零 D、非负数

查看试题解析
7. 如图，AB是半圆的直径，点C是弧AB的中点，点E是弧AC的中点，连接EB，CA交于点F，则 $\frac{E F}{B F}$ ＝（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、1﹣ $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
8. 直线y＝kx+b不经过第三象限，a＞e，且A（a，m）、B（e，n）、C（﹣m，c）、D（﹣n，d）这四点都在直线上，则（m﹣n）（c﹣d）³是（）

A、正数 B、负数 C、非正数 D、无法确定

查看试题解析

二、填空题（共8小题，4*8=32）

9. 写出直线y＝﹣2x﹣3关于y轴对称的直线的解析式．

查看试题解析
10. 甲、乙两点在边长为100m的正方形ABCD上按顺时针方向运动，甲的速度为5m/秒，乙的速度为10m/秒，甲从A点出发，乙从CD边的中点出发，则经过秒，甲乙两点第一次在同一边上．

查看试题解析
11. 已知，a+b=4n+2，ab=1，若19a²+147ab+19b²的值为2009，则n= ．

查看试题解析
12. 将自然数按以下规律排列，则位于第六行第四十五列的数是．

查看试题解析
13. 如图，直线y＝﹣ $\frac{4}{3}$ x+8与x轴，y轴分别交于点A和B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的解析式为．

查看试题解析
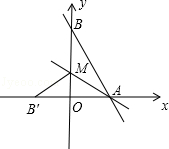14. 已知3，a，4，b，5这五个数据，其中a，b是方程x²﹣3x+2＝0的两个根，则这五个数据的标准差是．

查看试题解析
15. 如图，▱ABCD中，E为AD的中点．已知△DEF的面积为1，则▱ABCD的面积为．

查看试题解析
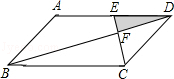16. 如图，⊙P的半径为2，圆心P在函数 $y = \frac{6}{x}$ （x＞0）的图象上运动，当⊙P与x轴相切时，点P的坐标为．

查看试题解析

三、解答题（共5小题，56分）

17. 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象进行以下探究：

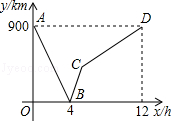
信息读取：

(1)、甲、乙两地之间的距离为km；

(2)、请解释图中点B的实际意义；
图象理解：

(3)、求慢车和快车的速度；

(4)、求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；
问题解决：

(5)、若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？

查看试题解析
18. 如图，已知直线y＝﹣m（x﹣4）（m＞0）与x轴、y轴分别交于A、B两点，以OA为直径作半圆，圆心为C．过A作x轴的垂线AT，M是线段OB上一动点（与O点不重合），过M点作半圆的切线交直线AT于N，交AB于F，切点为P．连接CN、CM．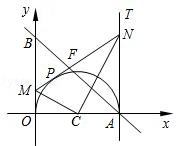

(1)、证明：∠MCN＝90°；

(2)、设OM＝x，AN＝y，求y关于x的函数解析式；

(3)、若OM＝1，当m为何值时，直线AB恰好平分梯形OMNA的面积．

查看试题解析
19. 某旅游胜地欲开发一座景观山．从山的侧面进行勘测，迎面山坡线ABC由同一平面内的两段抛物线组成，其中AB所在的抛物线以A为顶点、开口向下，BC所在的抛物线以C为顶点、开口向上．以过山脚（点C）的水平线为x轴、过山顶（点A）的铅垂线为y轴建立平面直角坐标系如图（单位：百米）．已知AB所在抛物线的解析式为y＝﹣ $\frac{1}{4}$ x²+8，BC所在抛物线的解析式为y＝ $\frac{1}{4}$ （x﹣8）² ，且已知B（m，4）．

(1)、设P（x，y）是山坡线AB上任意一点，用y表示x，并求点B的坐标；

(2)、从山顶开始、沿迎面山坡往山下铺设观景台阶．这种台阶每级的高度为20厘米，长度因坡度的大小而定，但不得小于20厘米，每级台阶的两端点在坡面上（见图）．
①分别求出前三级台阶的长度（精确到厘米）；

②这种台阶不能一直铺到山脚，为什么？

(3)、在山坡上的700米高度（点D）处恰好有一小块平地，可以用来建造索道站．索道的起点选择在山脚水平线上的点E处，OE＝1600（米）．假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线，解析式为y＝ $\frac{1}{28}$ （x﹣16）² ．试求索道的最大悬空高度．

查看试题解析
20. 如图，直线l： $y = \frac{4}{3} x + 4$ 交x轴、y轴于A、B点，四边形ABCD为等腰梯形，BC∥AD，AD＝12．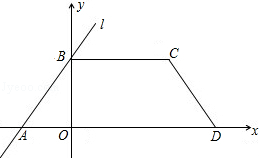

(1)、写出点A、B、C的坐标；

(2)、若直线l沿x轴正方向平移m（m＞0）个单位长度，与BC、AD分别交于E、F点，当四边形ABEF的面积为24时，求直线EF的表达式以及点F到腰CD的距离；

(3)、若B点沿BC方向，从B到C运动，速度为每秒1个单位长度，A点同时沿AD方向，从A到D运动，速度为每秒2个单位长度，经过t秒后，A到达P处，B到达Q处，问：是否存在t，使得△PQD为直角三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析
21. 阅读理解：
课外兴趣小组活动时，老师提出了如下问题：

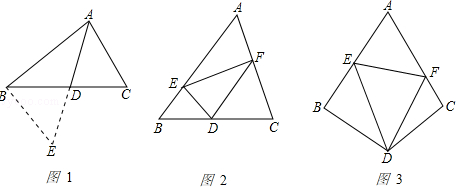
如图1，△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．

小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE＝AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．

感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．

(1)、问题解决：
受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

①求证：BE+CF＞EF；

②若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明；

(2)、问题拓展：
如图3，在四边形ABDC中，∠B+∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

查看试题解析