浙教版2018-2019学年重点高中自主招生数学模拟试卷（四）

试卷更新日期：2019-04-29 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 如果一个三角形的三边长分别为1，k，3，则化简 $7 - \sqrt{4 k^{2} - 36 k + 81} - | 2 k - 3 |$ 的结果是（）

A、﹣5 B、1 C、13 D、19﹣4k

查看试题解析
2. 设x为正整数，若x+1是完全平方数，则它前面的一个完全平方数是（）

A、x B、 $x - 2 \sqrt{x} + 1$ C、 $x - 2 \sqrt{x + 1} + 1$ D、 $x - 2 \sqrt{x + 1} + 2$

查看试题解析
3. 如图，A，B，C，D是直线L上顺次四点，M，N分别是AB，CD的中点，且MN=6cm，BC=1cm，则AD的长等于（）

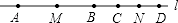A、10cm B、11cm C、12cm D、13cm

查看试题解析
4. 如图，⊙O₁与⊙O₂的半径均为5，⊙O₁的两条弦长分别为6和8，⊙O₂的两条弦长均为7，则图中阴影部分面积的大小关系为（）

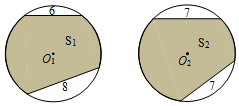A、S₁＞S₂ B、S₁＜S₂ C、S₁=S₂ D、无法确定

查看试题解析
5. 已知x=2是关于x的一元一次方程mx+2=0的解，则m的值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
6. 某单位在一快餐店订了22盒盒饭，共花费183元，盒饭共有甲、乙、丙三种，它们的单价分别为10元、8元、5元．那么可能的不同订餐方案有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，点C为线段AB上一点，且AC=2CB，以AC、CB为边在AB的同侧作等边△ADC和等边△EBC，连接DB、AE交于点F，连接FC，若FC=3，设DF=a、EF=b，则a、b满足（）

A、a=2b+1 B、a=2b+2 C、a=2b D、a=2b+3

查看试题解析
8. 设关于x的方程ax²+（a+2）x+9a=0，有两个不相等的实数根x₁、x₂ ，且x₁＜1＜x₂ ，那么实数a的取值范围是（）

A、 $a < - \frac{2}{11}$ B、 $\frac{2}{7} < a < \frac{2}{5}$ C、 $a > \frac{2}{5}$ D、 $- \frac{2}{11} < a < 0$

查看试题解析
9. 如图，已知在△ABC中，点D，E分别在边AB，AC上，DE∥BC，AD：BD=2：1，点F在AC上，AF：FC=1：2，联结BF，交DE于点G，那么DG：GE等于（）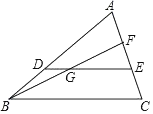

A、1：2 B、1：3 C、2：3 D、2：5．

查看试题解析
10. 7条长度均为整数厘米的线段：a₁ ， a₂ ， a₃ ， a₄ ， a₅ ， a₆ ， a₇ ，满足a₁＜a₂＜a₃＜a₄＜a₅＜a₆＜a₇ ，且这7条线段中的任意3条都不能构成三角形．若a₁=1厘米，a₇=21厘米，则a₆能取的值是（）

A、18厘米 B、13厘米 C、8厘米 D、5厘米

查看试题解析

二、填空题（共8小题，满分40分，每小题5分）

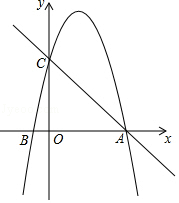
11. 若不等式组 ${\begin{matrix} 2 x - 3 \geq 0 \\ x \leq m \end{matrix}$ 无解，则m的取值范围是．

查看试题解析
12. 如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．过点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，点P的坐标为．

查看试题解析
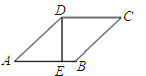
13.
如图，在菱形ABCD中，DE⊥AB ，垂足是E ， DE=6，sinA= $\frac{3}{5}$ ，则菱形ABCD的周长是

查看试题解析
14. 已知asinθ+cosθ=1，且bsinθ﹣cosθ=1，（其中θ是锐角），则ab= ．

查看试题解析
15. 设x是实数，则函数y=|x﹣1|+|x﹣2|﹣|x﹣3|的最小值是．

查看试题解析
16. 如图，在Rt△ABC中，∠BAC=90°，若AB=3cm，BC=5cm，E在AB上且AE=1cm，点P从B点出发，以1cm/s的速度沿BC→CA运动至A点停止，设运动的时间为ts，当t= ， △BEP为等腰三角形．

查看试题解析
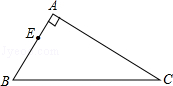17. 方程x²﹣4x+3a²﹣2=0在区间[﹣1，1]上有实根．则实数a的取值范围是．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，BC＝a₀ ， ∠A＝θ（其中a₀ ， θ为常数），把边长依次为a₁ ， a₂ ， a₃ ， …，a₁₀的10个正方形依次放入Rt△ABC中，第一个正方形CM₁P₁N₁的顶点分别放在Rt△ABC的各边上；第二个正方形M₁M₂P₂N₂的顶点分别放在Rt△AP₁M₁的各边上，…，其他正方形依次放入，则第10个正方形的边长a₁₀＝．（用a₀ ， θ表示）

查看试题解析

三、解答题（共4小题，满分50分）

19. 设x₁ ， x₂是关于x的一元二次方程x²+2ax+a²+4a﹣2=0的两实根，当a为何值时，x₁²+x₂²有最小值？最小值是多少？

查看试题解析
20. 如图1，等腰直角三角形ABC的腰长是2，∠ABC=90度．以AB为直径作半圆O，M是BC上一动点（不运动至B、C两点），过点M引半圆为O的切线，切点是P，过点A作AB的垂线AN，交切线MP于点N，AC与ON、MN分别交于点E、F．

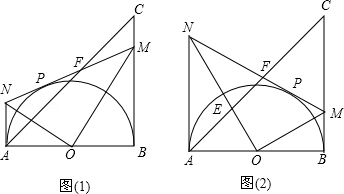(1)、证明：△MON是直角三角形；

(2)、当BM= $\sqrt{3}$ 时，求 $\frac{C F}{A F}$ 的值（结果不取近似值）；

(3)、当BM= $\frac{\sqrt{3}}{3}$ 时（图2），判断△AEO与△CMF是否相似？如果相似，请证明；如果不相似，请说明理由．

查看试题解析
21. 如图1，在平面直角坐标系xOy中，直线l： $y = \frac{3}{4} x + n$ 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点B，且与直线l的另一个交点为C（4，n）．

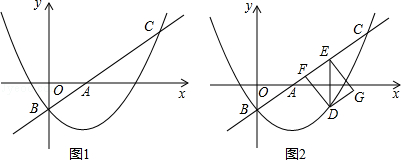(1)、求n的值和抛物线的解析式；

(2)、点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

(3)、M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁ ．若△A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的横坐标．

查看试题解析
22. 如图，已知二次函数y=﹣x²+bx+c（c＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB=OC=3，顶点为M．

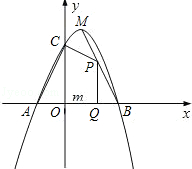(1)、求二次函数的解析式；

(2)、点P为线段BM上的一个动点，过点P作x轴的垂线PQ，垂足为Q，若OQ=m，四边形ACPQ的面积为S，求S关于m的函数解析式，并写出m的取值范围；

(3)、探索：线段BM上是否存在点N，使△NMC为等腰三角形？如果存在，求出点N的坐标；如果不存在，请说明理由．

查看试题解析