浙教版2018-2019学年重点高中自主招生数学模拟试卷(三)
试卷更新日期:2019-04-29 类型:中考模拟
一、选择题(共6小题,满分30分,每小题5分)
-
1. 已知 =1, =2, =3,则x的值是( )
A、1 B、 C、 D、﹣12. 已知,抛物线y=ax2+bx+c的部分图象如图,则下列说法:①对称轴是直线x=1;②当﹣1<x<3时,y<0;③a+b+c=﹣4;④方程ax2+bx+c+5=0无实数根.其中正确的有( )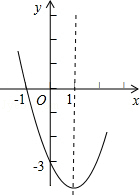 A、1个 B、2个 C、3个 D、4个3. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、1个 B、2个 C、3个 D、4个3. 函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A、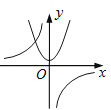 B、
B、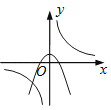 C、
C、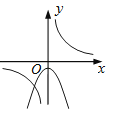 D、
D、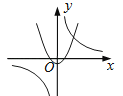 4. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
4. 如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ) A、点A B、点B C、AB之间 D、BC之间5. 如图,A,B,C,D是直线L上顺次四点,M,N分别是AB,CD的中点,且MN=6cm,BC=1cm,则AD的长等于( )
A、点A B、点B C、AB之间 D、BC之间5. 如图,A,B,C,D是直线L上顺次四点,M,N分别是AB,CD的中点,且MN=6cm,BC=1cm,则AD的长等于( )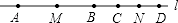 A、10cm B、11cm C、12cm D、13cm6. x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足下列两个等式:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2+…+(x20﹣1)2=32,则这列数中1的个数为( )A、8 B、10 C、12 D、14
A、10cm B、11cm C、12cm D、13cm6. x1、x2、x3、…x20是20个由1,0,﹣1组成的数,且满足下列两个等式:①x1+x2+x3+…+x20=4,②(x1﹣1)2+(x2﹣1)2+(x3﹣1)2+…+(x20﹣1)2=32,则这列数中1的个数为( )A、8 B、10 C、12 D、14二、填空题(共8小题,满分40分,每小题5分)
-
7. 化简: = .8. 已知mn+p2+4=0,m﹣n=4,则m+n的值是 .9. 如图,AB、AC是⊙O的两条弦,过点C的切线交OB的延长线于点D,若∠A=24°,则∠D的度数为 .
 10. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,请根据这组数的规律写出第10个数是 .
10. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,请根据这组数的规律写出第10个数是 .
11. 由小到大排列的一组数据x1 , x2 , x3 , x4 , x5 , 其中每个数据都小于﹣1,则对于1,x1 , ﹣x2 , x3 , ﹣x4 , x5的中位数可表示为 .12. 分解因式:x2﹣2x﹣2y2+4y﹣xy= .13. 如图,在x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是 .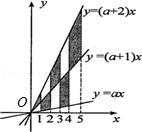 14. 按下面程序计算,若开始输入x的值为正数,最后输出的结果为656,则满足条件所有x的值是 .
14. 按下面程序计算,若开始输入x的值为正数,最后输出的结果为656,则满足条件所有x的值是 .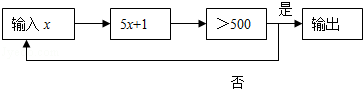
三、解答题(共5小题,满分80分)
-
15. 已知y关于x的函数:y=(k﹣2)x2﹣2(k﹣1)x+k+1中满足k≤3.(1)、求证:此函数图象与x轴总有交点;(2)、当关于z的方程 有增根时,求上述函数图象与x轴的交点坐标.16. 任意给定一个非零数m,按下列程序计算.
 (1)、请用含m的代数式表示该计算程序,并给予化简.(2)、当输入的m=﹣1时,求代数式的值.17. 设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2 ,
(1)、请用含m的代数式表示该计算程序,并给予化简.(2)、当输入的m=﹣1时,求代数式的值.17. 设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2 ,
(1)、若x12+x22=6,求m值;
(2)、令T= ,求T的取值范围.
18. 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点E的位置,连接BE,若BC=6cm.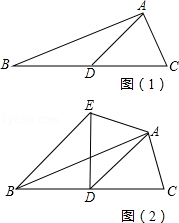 (1)、求BE的长;(2)、当AD=4cm时,求四边形BDAE的面积.19. 如图1,在平面直角坐标系xOy中,直线l: 与x轴、y轴分别交于点A和点B(0,﹣1),抛物线 经过点B,且与直线l的另一个交点为C(4,n).
(1)、求BE的长;(2)、当AD=4cm时,求四边形BDAE的面积.19. 如图1,在平面直角坐标系xOy中,直线l: 与x轴、y轴分别交于点A和点B(0,﹣1),抛物线 经过点B,且与直线l的另一个交点为C(4,n).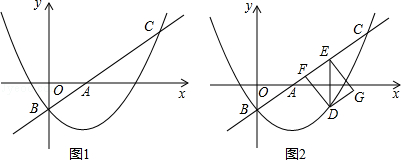 (1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1 . 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.
(1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1 . 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.