浙教版2018-2019学年重点高中自主招生数学模拟试卷（一）

试卷更新日期：2019-04-29 类型：中考模拟

进入出卷网下载

一、选择题（共8小题，4*8=32）

1. 实数b满足|b|＜3，并且有实数a，a＜b恒成立，a的取值范围是（）

A、小于或等于3的实数 B、小于3的实数 C、小于或等于﹣3的实数 D、小于﹣3的实数

查看试题解析
2. 代数式 $\sqrt{x^{2} + 4} + \sqrt{{(12 - x)}^{2} + 9}$ 的最小值为（）

A、12 B、13 C、14 D、11

查看试题解析
3. 已知关于x的方程 $\frac{x + a}{x - 3} = - 1$ 有正根，则实数a的取值范围是（）

A、a＜0且a≠﹣3 B、a＞0 C、a＜﹣3 D、a＜3且a≠﹣3

查看试题解析
4.
如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm² ，则该半圆的半径为（　　）

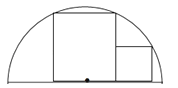A、(4+ $\sqrt{5}$ )cm B、9 cm C、4 $\sqrt{5}$ cm D、6 $\sqrt{2}$ cm

查看试题解析
5. 如图：将一个矩形纸片ABCD，沿着BE折叠，使C，D点分别落在点C₁ ， D₁处．若∠C₁BA＝50°，则∠ABE的度数为（）

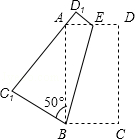A、15° B、20° C、25° D、30°

查看试题解析
6. 观察图中正方形四个顶点所标的规律，可知2012应标在（）

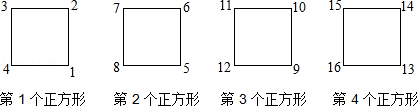A、第502个正方形的左下角 B、第502个正方形的右下角 C、第503个正方形的左上角 D、第503个正方形的左下角

查看试题解析
7. 100人共有2000元人民币，其中任意10人的钱数的和不超过380元．那么一个人最多有（）元．

A、 216 B、218 C、238 D、236

查看试题解析
8. 如图，正方形ABCD的边AB＝1， $\hat{B D}$ 和 $\hat{A C}$ 都是以1为半径的圆弧，则无阴影两部分的面积之差是（）

A、 $\frac{π}{2} - 1$ B、1﹣ $\frac{π}{4}$ C、 $\frac{π}{3}$ ﹣1 D、1﹣ $\frac{π}{6}$

查看试题解析

二、填空题（共8小题，4*8=32）

9. 两个反比例函数y＝ $\frac{3}{x}$ ，y＝ $\frac{6}{x}$ 在第一象限内的图象如图所示．点P₁ ， P₂ ， P₃、…、P₂₀₀₇在反比例函数y＝ $\frac{6}{x}$ 上，它们的横坐标分别为x₁、x₂、x₃、…、x₂₀₀₇ ，纵坐标分别是1，3，5…共2007个连续奇数，过P₁ ， P₂ ， P₃、…、P₂₀₀₇分别作y轴的平行线，与y＝ $\frac{3}{x}$ 的图象交点依次为Q₁（x₁′，y₁′）、Q₁（x₂′，y₂′）、…、Q₂（x₂₀₀₇′，y₂₀₀₇′），则|P₂₀₀₇Q₂₀₀₇|＝．

查看试题解析
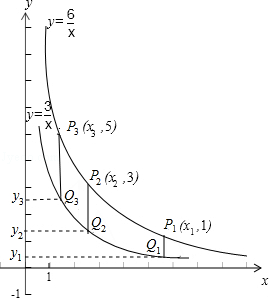10. 多项式6x³﹣11x²+x+4可分解为

查看试题解析
11. 已知x= $\sqrt[3]{4 (\sqrt{5} + 1)} - \sqrt[3]{4 (\sqrt{5} - 1)}$ ，则x³+12x的算术平方根是．

查看试题解析
12. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）（4，0）根据这个规律探索可得，第100个点的坐标为．

查看试题解析
13. 如图，已知二次函数y₁＝ax²+bx+c（a≠0）与一次函数y₂＝kx+m（k≠0）的图象相交于点A（﹣2，4），B（8，2），则关于x的不等式ax²+（b﹣k）x+c﹣m＞0的解集是．

查看试题解析
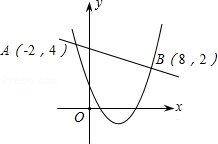14. 在平面直角坐标系中，横坐标与纵坐标都是整数的点（x，y）称为整点，如果将二次函数 $y = - x^{2} + 8 x - \frac{39}{4}$ 的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有个．

查看试题解析
15. 如图所示：两个同心圆，半径分别是 $2 \sqrt{6}$ 和 $4 \sqrt{3}$ ，矩形ABCD边AB，CD分别为两圆的弦，当矩形ABCD面积取最大值时，矩形ABCD的周长是．

查看试题解析
16. 如图，Rt△ABC中，∠BCA＝90°，∠BAC＝30°，AB＝6．△ABC以点B为中心逆时针旋转，使点C旋转至AB边延长线上的C′处，那么AC边转过的图形（图中阴影部分）的面积是．

查看试题解析

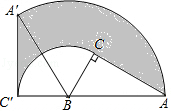
三、解答题（共5小题，56分）

17. 如图，四边形ABCD为圆内接四边形，对角线AC、BD交于点E，延长DA、CB交于点F，且∠CAD＝60°，DC＝DE．

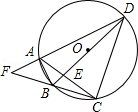
求证：

(1)、AB＝AF；

(2)、A为△BEF的外心（即△BEF外接圆的圆心）．

查看试题解析
18. 一个家庭有3个孩子，

(1)、求这个家庭有2个男孩和1个女孩的概率；

(2)、求这个家庭至少有一个男孩的概率．

查看试题解析
19. 如图，OA和OB是⊙O的半径，并且OA⊥OB．P是OA上的任意一点，BP的延长线交⊙O于点Q，点R在OA的延长线上，且RP＝RQ．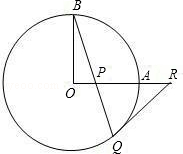

(1)、求证：RQ是⊙O的切线；

(2)、求证：OB²＝PB•PQ+OP²；

(3)、当RA≤OA时，试确定 ∠OBQ 的取值范围．

查看试题解析
20. 如图1，一张三角形纸片ABC，∠ACB＝90°，AC＝8，BC＝6．沿斜边AB的中线CD把这张纸片剪成△AC₁D₁和△BC₂D₂两个三角形（如图2），将纸片△AC₁D₁沿直线D₂B（AB）方向平移（点A、D₁、D₂、B始终在同一直线上），当点D₁与点B重合时，停止平移．在平移过程中，C₁D₁与BC₂交于点E，AC₁与C₂D₂、BC₂分别交于点F、P．

(1)、当△AC₁D₁平移到如图3所示的位置时，猜想图中的D₁E与D₂F的数量关系，并证明你的猜想；

(2)、设平移距离D₂D₁为x，△AC₁D₁与△BC₂D₂重叠部分面积为y，请写出y与x的函数关系式，并求出函数y的最值．

查看试题解析
21. 平面上有n个点（n≥3，n为自然数），其中任何三点不在同一直线上．证明：一定存在三点，以这三点作为顶点的三角形中至少有一个内角不大于 $\frac{180^{°}}{n}$ ．

查看试题解析