浙江省绍兴市2019年中考数学预测卷3
试卷更新日期：2019-04-29 类型：中考模拟
一、选择题（本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）
-
1. （-2）2004+3×（-2）2003的值为 （ ）
A、-22003 B、22003 C、-22004 D、220042. 当x=1时，代数式x3+x+m的值是7，则当x=－1时，这个代数式的值是（ ）A、7 B、3 C、1 D、－73. 以下3个说法中：①在同一直线上的4点A、B、C、D只能表示5条不同的线段；②经过两点有一条直线，并且只有一条直线；③同一个锐角的补角一定大于它的余角．说法都正确的结论是（ ）A、②③ B、③ C、①② D、①4. 如图，直线m∥n，∠1=70°，∠2=30°，则∠A等于（ ）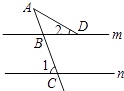
A、30° B、35° C、40° D、50°5. 在△ABC中，∠A=90°，AB=3cm，AC=4cm，若以A为圆心3cm为半径作⊙O，则BC与⊙O的位置关系是（ ）A、相交 B、相离 C、相切 D、不能确定6. 小岩打算购买气球装扮学校“毕业典礼”活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同．由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（ ）
A、19 B、18 C、16 D、157. 以下是某手机店1～4月份的两个统计图，分析统计图，对3、4月份三星手机的销售情况四个同学得出的以下四个结论，其中正确的为（ ）
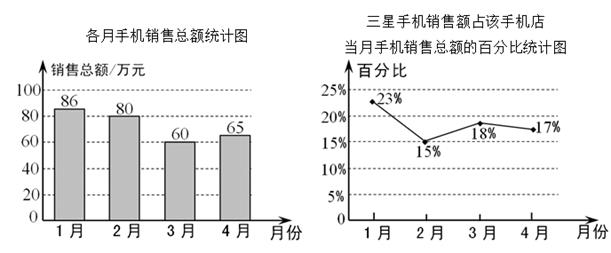A、4月份三星手机销售额为65万元 B、4月份三星手机销售额比3月份有所上升 C、4月份三星手机销售额比3月份有所下降 D、3月份与4月份的三星手机销售额无法比较，只能比较该店销售总额8.运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（ ）
A、x≥11 B、11≤x＜23 C、11＜x≤23 D、x≤239. 如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=3，DC=1，点P是AB上的动点，则PC+PD的最小值为（ ）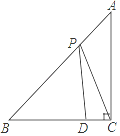
A、4 B、5 C、6 D、710. 如图，在▱ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF，其中正确结论的个数共有（ ）
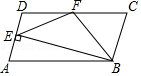A、1个 B、2个 C、3个 D、4个二、填空题（本大题共6小题，每小题5分，共30分）
-
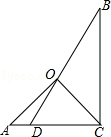
11. 从甲、乙两班分别任抽10名学生进行英语口语测验，其测试成绩 的方差是s甲2=13，s乙2=26，则班学生的成绩比较整齐.12. 如图，一副三角板△AOC和△BCD如图摆放，则∠AOB= ．
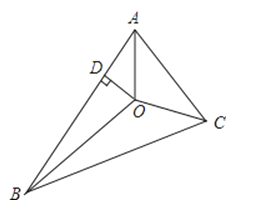
13.如图，△ABC的三条角平分线交于O点，已知△ABC的周长为20，OD⊥AB，OD=5，则△ABC的面积= ．
14. 如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立，根据图乙，利用面积的不同表示方法，仿照上边的式子写出一个等式 ．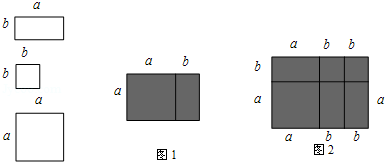
15. 已知关于x的方程 =m的解满足 （0＜n＜3），若y＞1，则m的取值范围是 ．16. 如图1，在△ABC中，∠BAC=90°，AB=AC=2 ，D、E两点分别在AC、BC上，且DE∥AB，DC=2 ，将△CDE绕点C顺时针旋转得到△CD′E′，如图2，点D、E对应点分别为D′、E′、D′、E′与AC相交于点M，当E′刚好落在边AB上时，△AMD′的面积为 ．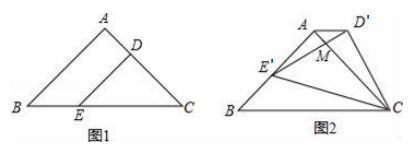
三、解答题（本大题共8小题，共80分）
-
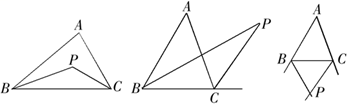
17.(1)、计算： ﹣ sin60°+|2﹣ |+(2)、解分式方程： +2=18. 如图，BP、CP分别是△ABC的内角或外角平分线，请你根据下面的三种情形分别画出点P到△ABC三边所在直线的距离．
19. 随着航母编队的成立，我国海军日益强大.2018年4月12日，中央军委在南海海域隆重举行海上阅兵，在阅兵之前我军加强了海上巡逻，如图，我军巡逻舰在某海域航行到A处时，该舰在观测点P的南偏东45°的方向上，且与观测点P的距离PA为400海里；巡逻舰继续沿正北方向航行一段时间后，到达位于观测点P的北偏东30°方向上的B处，问此时巡逻舰与观测点P的距离PB为多少海里？（参考数据： ≈1.414， ≈1.732，结果精确到1海里）．
20. 在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．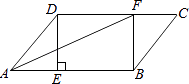
(1)、求证：四边形BFDE是矩形；(2)、若CF=3，BF=4，DF=5，求证：AF平分∠DAB．21. 某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
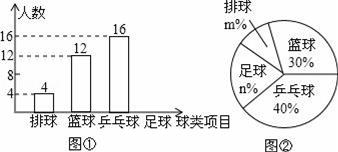(1)、求九（1）班的学生人数，并把条形统计图补充完整；(2)、扇形统计图中m= ， n= ， 表示“足球”的扇形的圆心角是度；(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．22. 如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A（ ，﹣2），反比例函数y= （x＞0）的图象过点A．
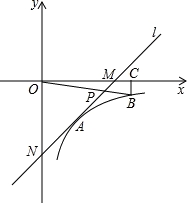(1)、求直线l的解析式；(2)、在函数y= （x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．23. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P顺时针旋转60°，得到线段PQ，连接BQ．
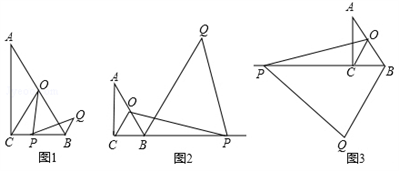(1)、如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．(2)、如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；(3)、如图3，当点P在BC延长线上时，若∠BPO=15°，BP=4，请求出BQ的长．24. 学校“百变魔方”社团准备购买A，B两种魔方，已知购买2个A种魔方和6个B种魔方共需130元，购买3个A种魔方和4个B种魔方所需款数相同．
(1)、求这两种魔方的单价；(2)、结合社员们的需求，社团决定购买A，B两种魔方共100个（其中A种魔方不超过50个）．某商店有两种优惠活动，如图所示．请根据以上信息，说明选择哪种优惠活动购买魔方更实惠．