浙江省绍兴市2019年中考数学预测卷2
试卷更新日期：2019-04-29 类型：中考模拟
一、选择题（本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）
-
1. ﹣ 的相反数是（ ）A、8 B、﹣8 C、 D、﹣2. 2012年伦敦奥运会上，中国选手吕小军在男子举重77公斤级比赛中，打破了原奥运会纪录，创造了新抓举纪录，成绩是175公斤，下列说法正确的是（ ）A、原来奥运会纪录是175公斤 B、原来奥运会纪录是77公斤 C、原来奥运会纪录小于77公斤 D、原来奥运会纪录小于175公斤3. 如图是底面为正方形的长方体，下面有关它的三个视图的说法正确的是（ ）
A、俯视图与主视图相同 B、左视图与主视图相同 C、左视图与俯视图相同 D、三个视图都相同4. 一个不透明的布袋里装有5个红球，2个白球，3个黄球，它们除颜色外其余都相同，从袋中任意摸出1个球，是黄球的概率为（ ）A、 B、 C、 D、5. 下列计算，结果等于a4的是（ ）A、a+3a B、a5﹣a C、（a2）2 D、a8÷a26.一次函数y=kx+b（k，b为常数，且k≠0）的图象如图所示，根据图象信息可求得关于x的方程kx+b=0的解为（ ）
A、x=﹣1 B、x=2 C、x=0 D、x=37. 如图，点D是BC边上一点且BD：DC=1：2，点F为线段AD上一点且AF：DF=1：2，BF的延长线交AC于E，则AE：AC=（ ）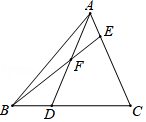
A、1：2 B、1：3 C、1：4 D、1：78. 如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是（ ）
A、
B、
C、
D、
9. 二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x1和x2 ， 且x1＜x2 ， 则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有（ ）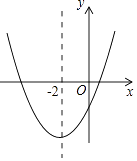
A、1个 B、2个 C、3个 D、4个10. 如图，▱ABCD的周长为32cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为 （ ）
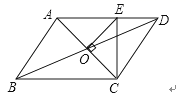A、24cm B、16cm C、8cm D、10cm二、填空题（本大题共6小题，每小题5分，共30分）
-
11. 化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）99= ．12. 为了开展“阳光体育”活动，某班计划购买甲、乙两种体育用品 每种体育用品都购买 ，其中甲种体育用品每件20元，乙种体育用品每件30元，共用去150元，请你设计一下，共有种购买方案．13.
如图，AB、CD是⊙O的两条弦，若∠AOB+∠C=180°，∠COD=∠A，则∠AOB=
14. 如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=4，M是AB边上一动点，N是AC边上的一动点，则MN+MC的最小值为 ．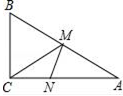
15. 已知矩形ABCD的四个顶点均在反比例函数y= 的图象上，且点A的横坐标是2，则矩形ABCD的面积为 ．16. 如图，在平面直角坐标系中，菱形OABC的一个顶点在原点O处，且∠AOC=60°，A点的坐标是（0，4），则直线AC的表达式是 ．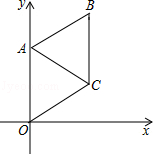
三、解答题（本大题共8小题，共80分）
-
17.
(1)、计算：|﹣2|﹣2cos60°+（ ）﹣1﹣（2018﹣ ）0(2)、先化简（1﹣ ）• ，再在1、2、3中选取一个适当的数代入求值．18. 某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）．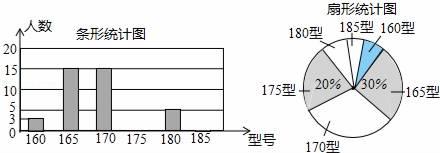
根据以上信息，解答下列问题：
(1)、该班共有多少名学生？其中穿175型校服的学生有多少？(2)、在条形统计图中，请把空缺部分补充完整．(3)、在扇形统计图中，请计算185型校服所对应的扇形圆心角的大小；(4)、求该班学生所穿校服型号的众数和中位数．19. 如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i=1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为33°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）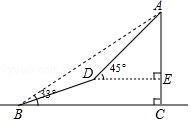
20. 已知二次函数y=x2﹣6x+8．(1)、将y=x2﹣6x+8化成y=a（x﹣h）2+k的形式；(2)、当0≤x≤4时，y的最小值是 ， 最大值是；(3)、当y＜0时，写出x的取值范围．21. 如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）
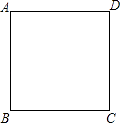22. 如图，△ABD和△ACE均为等腰直角三角形，A为公共直角顶点，过A作AF垂直CB交CB的延长线于F．
(1)、若AC=10，求四边形ABCD的面积；(2)、求证：CE=2AF．23. 如图，在平面直角坐标系中，△AOB的三个顶点的坐标分别是A（4，3），O（0，0），B（6，0）．点M是OB边上异于O，B的一动点，过点M作MN∥AB，点P是AB边上的任意点，连接AM，PM，PN，BN．设点M（x，0），△PMN的面积为S．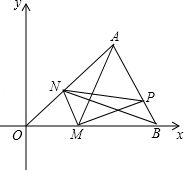
(1)、求出OA所在直线的解析式，并求出点M的坐标为（1，0）时，点N的坐标；(2)、求出S关于x的函数关系式，写出x的取值范围，并求出S的最大值；
(3)、若S：S△ANB=2：3时，求出此时N点的坐标．
24. 如图，点F在▱ABCD的对角线AC上，过点F，B分别作AB，AC的平行线相交于点E，连接BF，∠ABF=∠FBC+∠FCB．
(1)、求证：四边形ABEF是菱形；(2)、若BE=5，AD=8，sin∠CBE= ，求AC的长．